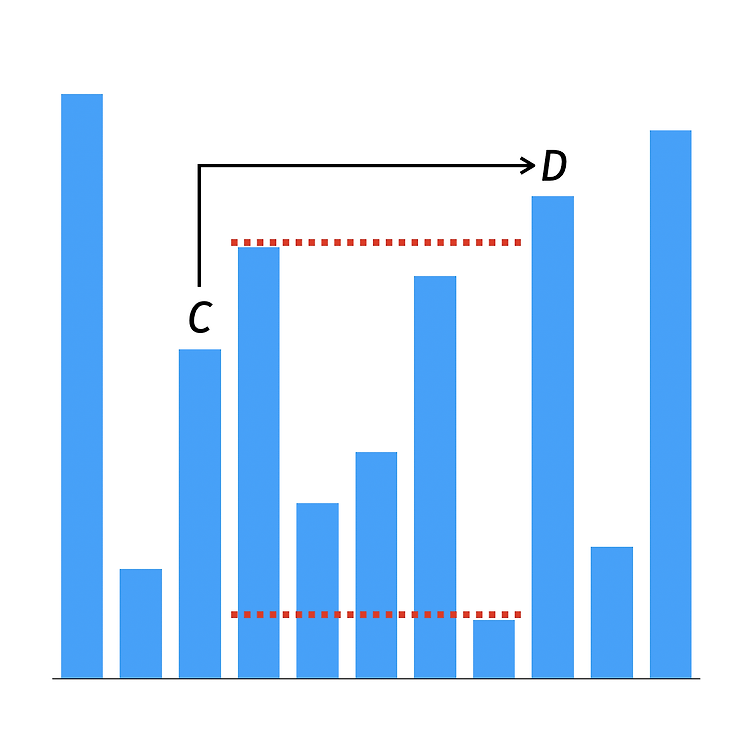
굉장히 재밌는 문제입니다. 부분문제 1 ~ 4 부분문제 1 : $C-B$를 반환하면 됩니다. 부분문제 2~4 : 그래프로 모델링하여 해결할 수 있습니다. 인접한 두 방향의 이동을 스택을 이용해 표현할 수 있고, 이로써 그래프를 만들어 둘 수 있습니다. 쿼리마다 multisoure BFS를 해주면 쉽게 답을 구할 수 있습니다. 부분문제 5 다시 표현하면 $[B,B]$에서 $[C,C]$로 가는 최단 경로를 찾거나, 도달 불가능함을 판별하는 문제입니다. $[A,B]$와 $[C,D]$에 대한 문제의 약한 버전이어서, 확실히 해결하면 정해로 직결될 법한 느낌이 나는 부분문제입니다. 관찰 1. $H_B < H_C$는 '도달 가능'의 필요조건입니다. 높이는 이동하는 과정에서 항상 엄격하게 높아지기 때문입니다. 관찰 ..

A에서는 디버깅에, B에서는 코딩에 시간을 쓰는 바람에 C를 대회 중에 해결하지 못해 아쉽습니다. 하지만 991등으로 마무리하여 티셔츠는 받게 되었습니다. 대회를 잘 봤는지와 무관하게, C번 문제가 꽤 흥미로워서 풀이를 남겨 놓고자 합니다. 우선, 문제 상황은 다음과 같습니다. 정점이 $N$개인 트리가 주어집니다. 각 정점 $v$에는 $M_v$개의 문자열이 주어집니다. 트리를 여러 개의 경로로 분할하되, 각 경로에 문자열 $s$가 포함되게 할 수 있다면 $s$는 mutually-learned 합니다. mutually-learned 한 문자열의 개수를 세는 것이 문제입니다. 모든 TC에 대해 $N$의 합은 $3\cdot 10^6$을 넘지 않습니다. 모든 TC에 대해 $\sum M_v$의 합은 $8\cdot..

문제 링크 고수들한테 교육적인 문제라고 생각한다. 부분문제 1 $W_i =0$ $(1 \le i \le N)$ 더보기 도달 불가능한 경우를 걸러내자. $H_{i-1} < D_{i}-D_{i-1}$이라면 $i-1$번 기둥에서 $i$번 기둥으로 이동하는 것이 불가능하다. 바닥에 닿기 때문이다. 그런 $i$가 존재하지 않는다면, 항상 $n$번 기둥까지 도달 가능하다. 걸러냈으니, 이제 문제에서 도달 가능함을 전제하고 풀이해 나갈 수 있다. 부분문제 4 $N \le 500$ $H_i \le 500$ $(1 \le i \le N)$ 더보기 $\mathrm{dp}(i,j):=i$번 기둥의 높이 $j$ 부분까지 이동하는데 걸리는 최소 시간 naive하게 다음과 같은 직관적인 점화식을 짤 수 있다. $\displays..

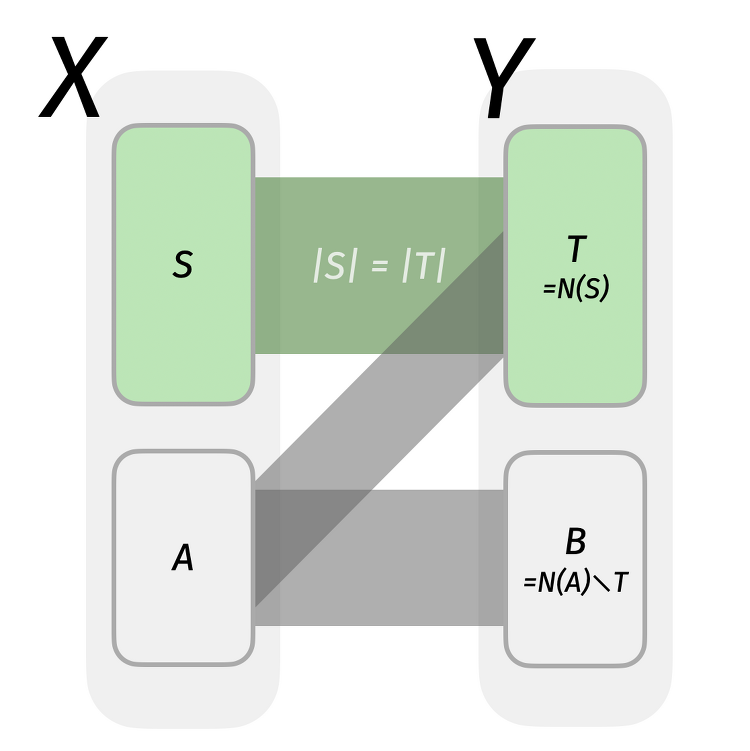
홀의 정리는 홀의 결혼 정리라고도 불리우는 정리로, 이분 매칭에서 유용하게 쓰이거나 다른 그래프 이론의 다양한 정리들의 증명에 도움이 된다. 홀의 정리를 증명해 보았다. 그냥 검색해봐도 되지만, 홀의 정리 문제 상황과 유사한 구조에서 비슷한 논리를 이끌어내는 문제가 존재하기 때문에 이를 대비하기 위해서 별도의 특수한 도구 없이 증명하는 것을 목표로 잡았다. Theorem: $($모든 $S\subset X$에 대해 $|S|\le |N(S)|$를 만족$) \iff (\exists X$에서 $Y$로의 완전 매칭$)$ $[\Leftarrow]$는 자명한 명제이므로, $[\Rightarrow]$만 증명한다. 좌변의 조건을 "홀의 조건"이라고 부르자. 수학적 귀납법으로 접근해 보자. $|X|$의 크기에 대한 귀납법..

별점 : 추천, [★★★☆★] 한국어 지문 : 링크, 번역이 구립니다 문제 요약 $n$-비트 정수 집합을 관리하는 자료구조가 있습니다. ($64$-비트 정수, $32$-비트 정수랑 같은 맥락이고 역시 $n$은 $2$의 거듭제곱) 이 자료구조에 일련의 정수 삽입 후, 컴파일을 거친 뒤, 일련의 정수 조회를 할 수 있습니다. 이때 컴파일 과정에서 버그가 발생합니다. 버그는 $n$ 비트의 순서가 어떤 순열에 따라 치환되는 형식으로 나타납니다. 정수 삽입을 $w$(write)번 이내, 정수 조회를 $r$(read)번 이내로 하여 버그가 갖는 순열을 알아내세요. 부분문제 1 (20점) 문제를 제대로 이해했는지 확인하는 부분문제입니다. 다음의 $8$개 정수를 삽입하면 최대 두 곳의 순열이 뒤바뀐 위치에서 비트 $1..

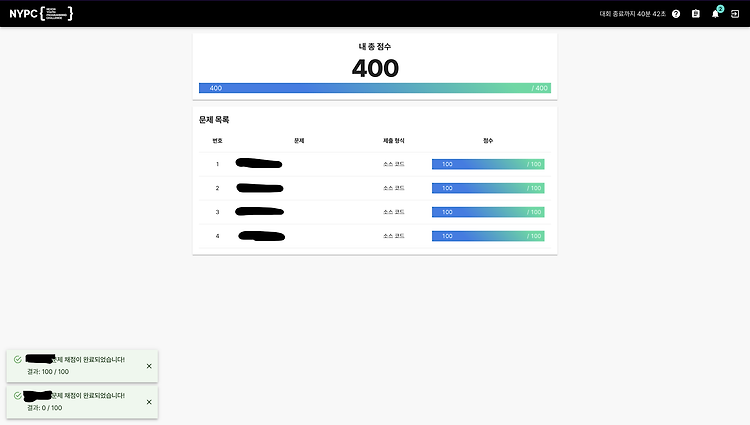
후기 보류 끝! 운영사무국의 지침에 따라, 풀이는 본선 이후에 정리하여 올리도록 하겠습니다. 더보기 운이 좋게도 NYPC Round 2-B에서 400점을 받고 본선에 진출했습니다. Round 2-A 후 기존의 전략에 반성 보통 저는 플래티넘 4 이하를 '쉽다'고 여깁니다. 그리고 플래티넘 3 ~ 2는 보통 '적당하다'고 여깁니다. 플래티넘 1 ~ 다이아 4는 유형이 나랑 잘 맞는다는 전제 하에 '해볼 만 하다'고 여기고, 그 위는 '부분 점수나 성실하게 긁어보자'는 마인드입니다. 따라서 저는 KOI 2023 2차와 Round 2-A에 '1, 2번 풀고 3, 4번 많이 긁는 전략'을 적용했습니다. Round 2-A 1, 2번은 40분 안에 풀어서 2번 난이도를 감안했을 때 뇌절 없이 잘 풀었다고 판단했습니..

대회 문제들은 여기서 확인하실 수 있습니다. 문제별로 제가 기여한 것들과 짧은 후기를 정리해보겠습니다. 전체적인 제안 검수를 딱 하려고 보니까 문제별로 tests가 150개를 넘어가던 걸로 기억합니다. 가뜩이나 Arena가 적용되어서 참가자 수가 많아질 것 같은데 tests가 이대로 많으면 안 될 것 같다고 줄여달라고 제안을 드렸습니다. 좀 늦게 제안했는데, 왜 그 전까지는 아무도 말을 안 꺼냈는지는 잘 모르겠네요.. 😅 또, 그래프 문제들의 조건에서 "$1\le i , j\le N$인 모든 $i$, $j$에 대해서 $i$번 구역에서 $j$번 구역으로 가능 경로가 항상 존재"를 " $1 \le i < j \le N$인 모든 $i$, $j$에 대해서 $i$번 구역과 $j$번 구역을 연결하는 경로가 존재"로..

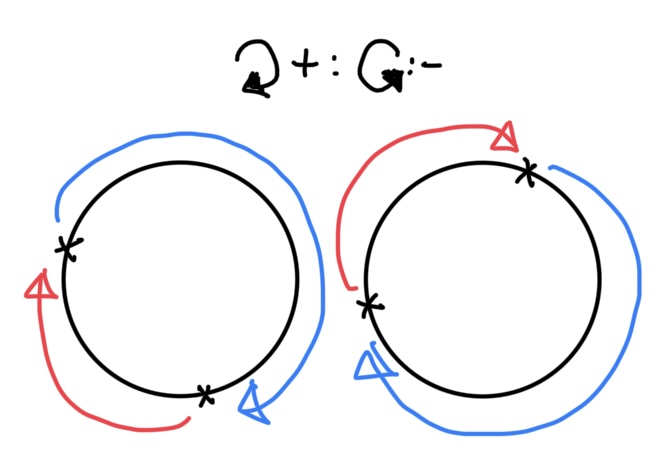
이 문제는 IOI 2022의 예비 문제로 출제된 문제이기 때문에, 백준 외에 이 문제의 채점을 지원하는 사이트를 찾지 못했습니다. 백준에서 채점 방식을 수정하여 올린 투스텝 문제의 특성상, 이 문제는 10초의 시간제한과 함께 채점 우선순위가 2입니다. 따라서 채점 속도가 상당히 느리니 이 점 유의하시기 바랍니다. 번역 빠져도 이해에 무리가 없는 길고 형식적인 예제 설명과 그레이더 피드백 방식 설명은 생략하여 번역했습니다. 문제의 핵심 $X = 1,2,\ldots,n$에서 크기 $k$의 조합 $Y = 1,2,\ldots,n$에서 크기 $k-1$의 순열 일 때, $X\overset f \to Y$인 $f$를 조건에 맞게 잘 구성하라는 문제입니다. 조건은 $f(x)=y$일 때, $y$가 $x$의 $k$개 원소..