이 문제는 IOI 2022의 예비 문제로 출제된 문제이기 때문에, 백준 외에 이 문제의 채점을 지원하는 사이트를 찾지 못했습니다.
백준에서 채점 방식을 수정하여 올린 투스텝 문제의 특성상, 이 문제는 10초의 시간제한과 함께 채점 우선순위가 2입니다. 따라서 채점 속도가 상당히 느리니 이 점 유의하시기 바랍니다.
번역
빠져도 이해에 무리가 없는 길고 형식적인 예제 설명과 그레이더 피드백 방식 설명은 생략하여 번역했습니다.
문제의 핵심
- $X = 1,2,\ldots,n$에서 크기 $k$의 조합
- $Y = 1,2,\ldots,n$에서 크기 $k-1$의 순열
일 때, $X\overset f \to Y$인 $f$를 조건에 맞게 잘 구성하라는 문제입니다.
조건은 $f(x)=y$일 때, $y$가 $x$의 $k$개 원소 중 정확히 하나의 원소만 빠진 상태로 구성되어야 한다는 것입니다.
이 조건을 만족시키는 것이 얼마나 힘든지는 모르겠으나, 일단 $|X|=\binom n k \le |Y|=\binom n {k-1} \times (k-1)!$이 부분문제의 모든 제약 조건에 부합하므로 가능할 것 같습니다. (놀랍게도 $|X|=|Y|$여도 문제를 효율적으로 해결하는 것이 가능하고, 이를 이용해 문제를 개조한 Hard 버전이 있습니다.)
또한 모든 $x$에 대해 $f(x)$로서 가능한 $y$의 후보는 $k!$개씩 있기 때문에 직관적으로 문제가 성립할 것 같다는 확신이 듭니다. 다만, 치역의 $y$에 대해 $f^{-1}(y)$의 후보는 $n-k$개씩 밖에 존재하지 않기 때문에 효과적으로 $x$를 추적해 낼 수 있는 방법을 함께 고려할 필요가 있을 것입니다.
부분문제 1: (5점) $N ≤ 3;$ $K = 2$
$|X|$와 $|Y|$ 모두 매우 작습니다.
직접 다 만들어 보시면 되겠습니다.
namespace sub1 {
vi encode() {
if (cards[0] == 1 and cards[1] == 2) return {1};
if (cards[0] == 2 and cards[1] == 3) return {2};
return {3};
}
int decode() {
if (cards == vi{1}) return 2;
if (cards == vi{2}) return 3;
return 1;
}
}
부분문제 2: (11점) $N ≤ 5;$ $K = 3$
이 경우는 손으로 계산하기가 쉽지 않습니다.
따라서 함수를 전처리 해 둔 다음 쿼리마다 대응되는 값들을 반환하는 식으로 구현하는 것이 제일 만만합니다.
함수를 전처리한다는 것은 즉, $X$와 $Y$를 다 나열하고 가능한 경우를 다 따져보는 방식이 되겠습니다.
namespace sub2 {
vector<vi> X, Y;
map<vi,vi> f;
map<vi,int> g;
bool ok(const vi &x, const vi &y) {
for (auto e : y) if (!count(all(x),e)) return false;
return true;
};
int missed(const vi &x, const vi &y) {
for (auto e : x) if (!count(all(y),e)) return e;
return 0;
};
void init() {
rep(b,0,(1<<n)-1) if (__builtin_popcount(b)==k) {
vi tmp; rep(i,1,n) if (b>>(i-1)&1) tmp.push_back(i);
X.push_back(tmp);
}
rep(i,1,n) rep(j,1,n) if (i != j) Y.push_back({i,j});
do {
auto it = begin(Y);
f.clear();
for (auto &x : X) {
for (; it != end(Y); ++it) {
if (ok(x,*it)) {
f[x] = *it++;
break;
}
}
}
if (siz(f) == siz(X)) break;
} while (next_permutation(all(X)));
for (auto &[x,y] : f) {
g[y] = missed(x,y);
}
}
vi encode() {
return f[cards];
}
int decode() {
return g[cards];
}
}
부분문제 3: (24점) $N ≤ 12;$ $K = 6$
관찰 1. $(k-1)! \ge n$를 만족합니다.
따라서 순열의 순서 정보를 통해서 빠진 카드의 정보에 대응시킬 수 있습니다.
구체적으로, 순열의 사전순 번호에 카드의 번호를 매칭시키면 됩니다.
namespace sub3 {
vi encode() {
int missed = cards.front();
vi res = cards;
res.erase(begin(res));
int cnt = 0;
do {
if (++cnt == missed) break;
} while (next_permutation(all(res)));
return res;
}
int decode() {
int missed = 0;
vi perm = cards;
sort(all(perm));
do {
++missed;
if (perm == cards) break;
} while (next_permutation(all(perm)));
return missed;
}
}
부분문제 4: (60점) $N ≤ 10\,000;$ $K = 8$
부분문제 3의 아이디어를 활용하고 싶습니다. 하지만 $(k-1)!=5040$으로, 근소한 차이로 $n$을 덮지 못합니다.
만약 정보를 절반으로 줄일 수만 있다면 부분문제 3의 아이디어에 합쳐서 문제를 풀어낼 수 있을 것입니다.
관찰 2. 비둘기집의 원리와 $7$로 나눈 나머지
어떤 정수를 특정/식별하는 방법으로 나머지를 분석하는 것이 많은 경우에 꽤 도움이 됩니다. 따라서 나머지를 적극적으로 정보에 이용하려 하는데, $k$가 작은 것이 눈에 띕니다.
저는 그런 이유로 카드들을 $7$로 나눈 나머지로 묶어 생각해 보았습니다. 그러면 비둘기집의 원리에 의해 반드시 하나 이상의 나머지에 대응되는 카드가 두 장 이상 존재하게 됩니다. 그리고 두 장 중 한 장은 투스텝 과정에서 보존되는데, 이건 $7$장의 카드 중 제일 앞에 놔둠으로써 $7$로 나눈 나머지를 전달할 수 있습니다. 그럼 나머지 $6$장은 $7$로 나눈 몫을 저장해야 합니다. 결국 $10000$을 $10000/7$로 줄였지만 표현할 수 있는 순열은 $6!=720$이기 때문에 별다른 성과는 없습니다.
관찰 3. mod를 원호로 보고 짧은 호의 길이에 주목
mod를 다룰 때 원을 생각하면 직관적으로 다루기가 쉽습니다. 일단 $10000$ 대신 $10010$로 나눈 나머지로 다루기로 합시다. 왜냐하면 $10000$은 $7$의 배수가 아니기 때문이죠.
그다음 시계방향으로 나머지 $0, 1, 2, \ldots, 10009$를 나열했다고 생각합시다. 이 중 $7$로 나눈 나머지가 동일한 두 카드를 잡고 하나를 다른 하나로 표현해야 된다는 목적을 갖고 보면, 아래와 같이 $(a-b) \bmod 10010$과 $(b-a)\bmod 10010$중 더 작은 것은 $10010/2=5005$ 이하가 될 수밖에 없다는 것에 주목할 수 있습니다. 여기서 $a$와 $b$가 뒤바뀌어도 $7$로 나눈 나머지는 같기 때문에 선택적으로 $a$와 $b$를 교환하여 $(b-a)\bmod 10010$가 더 작도록 고정시킬 수 있습니다.
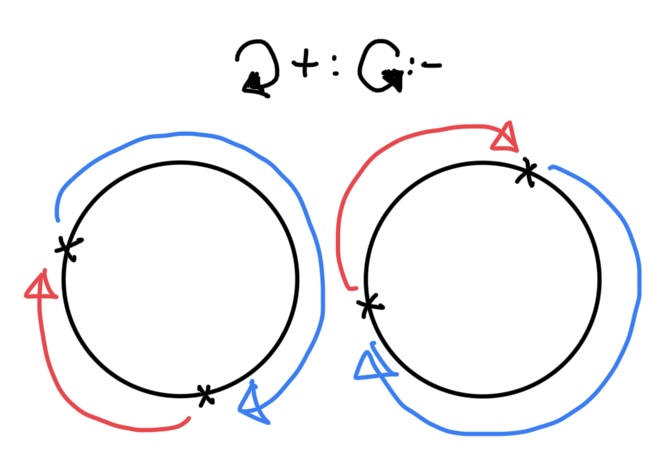
그럼 $7$장의 카드 중 첫 번째 카드는 $a$, 뒤의 $6$장의 카드는 $d=\left\lfloor\frac{(b-a)\bmod 10010}7\right\rfloor$번째 순열을 표현하도록 할 수 있습니다. 카드 복구는 $(a+7d)\bmod 10010$로 처리하면 됩니다. $d<10010/7/2=715$이므로 $6!=720$ 안에 표현되어 올바릅니다.
namespace sub4 {
vi encode() {
vector<int> cnt(7);
for (auto c : cards) cnt[c%7]++;
int a=-1, b=-1;
for (auto c : cards) if (cnt[c%7]>=2) {
if (a < 0) a = c;
else if (c%7 == a%7) b = c;
}
assert(a > 0 and b > 0);
// a < b
// [a,a+5005)에 b가 있는 경우
vi res; int express;
a--, b--;
assert(a < b);
if (b < min(10010,a+5005)) res.push_back(a+1), express = (b-a+10010)%10010; // b ∈ [a,a+5005)
else res.push_back(b+1), express = (a-b+10010)%10010; // b ∉ [a,a+5005)
a++, b++;
for (auto c : cards) if (c != a and c != b) res.push_back(c);
int i = 0;
do {
if (++i == express/7) break;
} while (next_permutation(1+all(res)));
return res;
}
int decode() {
int term = 0;
vi perm = cards;
sort(1+all(perm));
do {
++term;
if (perm == cards) break;
} while (next_permutation(1+all(perm)));
return (perm[0]+term*7)%10010 ? : 10010;
}
}
전체 코드
서브태스크마다 별개의 namespace로 감싸서 구현하면 코드가 정돈된다고 생각합니다.
따라서 전체 코드는 각 namespace의 solve를 호출하는 식으로 구성하였습니다.
#include "cards.h"
#include <bits/stdc++.h>
using namespace std; using ii = pair<int,int>; using ll = long long; using vi = vector<int>;
#define rep(i,a,b) for (auto i = (a); i <= (b); ++i)
#define per(i,a,b) for (auto i = (b); i >= (a); --i)
#define all(x) begin(x), end(x)
#define siz(x) int((x).size())
#define Mup(x,y) x = max(x,y)
#define mup(x,y) x = min(x,y)
#define fi first
#define se second
#define dbg(...) fprintf(stderr,__VA_ARGS__)
int n, k;
vi cards;
namespace sub1 {...}
namespace sub2 {...}
namespace sub3 {...}
namespace sub4 {...}
void init_magician(int _n, int _k) {
n=_n,k=_k;
if (k == 3) sub2::init();
}
void init_assistant(int _n, int _k) {
n=_n,k=_k;
if (k == 3) sub2::init();
}
vi choose_cards(vi _cards) {
cards = _cards;
if (k == 2) return sub1::encode();
if (k == 3) return sub2::encode();
if (k == 6) return sub3::encode();
if (k == 8) return sub4::encode();
assert(0);
}
int find_discarded_card(vi _cards) {
cards = _cards;
if (k == 2) return sub1::decode();
if (k == 3) return sub2::decode();
if (k == 6) return sub3::decode();
if (k == 8) return sub4::decode();
assert(0);
}'PS 문제들' 카테고리의 다른 글
| [Meta Hacker Cup 2023] C. Wiki Race (2) | 2023.10.22 |
|---|---|
| [IOI 2016 Day 2] Unscrambling a Messy Bug (BOJ 20089) ★ (0) | 2023.09.27 |
| [IOI 2011 Day 2] Parrots (BOJ 20137) (0) | 2023.07.29 |
| [KAIST Run 2023] Merging Branches (BOJ 28056) ★ (0) | 2023.07.02 |
| [KTSC 2023 #1] 던전 (BOJ 27508) (0) | 2023.03.15 |
