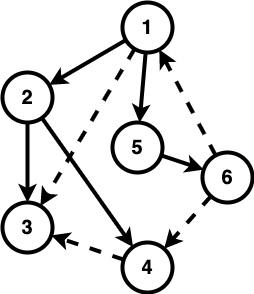
이 블로그의 "그래프에 관하여" 시리즈의 첫 번째 카테고리, ❮DFS 트리❯의 개요이다. DFS 트리는 DFS를 응용한 다양한 알고리즘들을 이해하기 위한 좋은 표현법이자 도구이다. 조금 어려운 감이 있지만 꼼꼼히 이해한다면 큰 도움이 될 것이라고 생각한다. DFS 트리/포레스트란? 어떤 연결 그래프에서 DFS 순회하는 과정을 그렸을 때 나타나는 유향 신장 트리(directed spanning tree)를 DFS 트리라고 한다. 당연히 여러 개가 존재할 수 있다. 연결 그래프가 아닐 경우에는 각 연결 컴포넌트마다 DFS 트리를 만들 수 있으니 DFS 포레스트로 확장해서 생각할 수 있다. 유향 그래프일 경우, DFS 트리의 간선들을 네 가지로 분류할 수 있다. 트리 간선(tree edge): DFS 트리에 ..

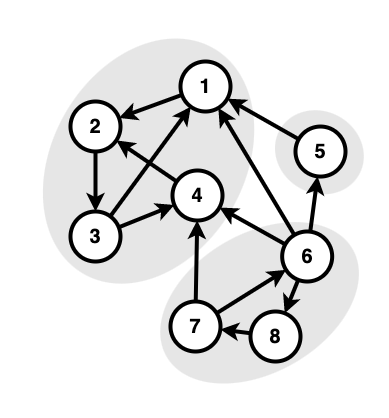
이 블로그의 "그래프에 관하여" 시리즈의 첫 번째 카테고리, ❮DFS 트리❯에서 다루는 첫 번째 주제이다. 편의를 위해 다음 표현을 정의하자. 정점 $v$의 방문 시작 시각: $s(v)$ 정점 $v$의 방문 종료 시각: $f(v)$ SCC란? 어떤 방향 그래프가 모든 정점에 대해, 다른 모든 정점으로 갈 수 있다면 강하게 결합(strongly connected)되었다고 한다. 모든 방향 그래프는 SCC(strongly connected component; 강결합 컴포넌트)로 나눌 수 있다. SCC란 모든 정점에서 다른 모든 정점으로 갈 수 있는 최대 크기의 정점 집합을 의미한다. 각 SCC를 새로운 정점으로 하고, 그 안의 모든 정점들에서 나가는 간선을 새로운 정점의 간선으로 갖게 하여 컴포넌트 그래프(..

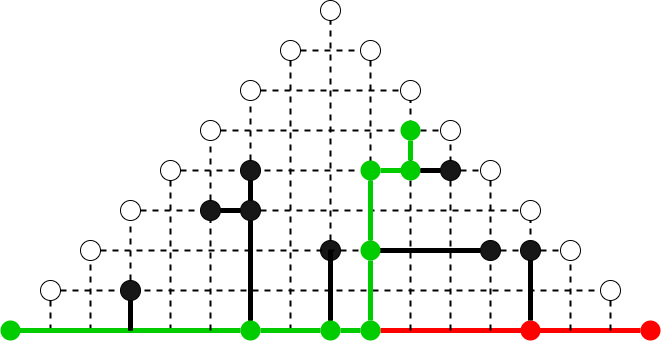
트리의 지름을 구하는 방법은 다음의 몇 가지가 있다. 동적 계획법을 이용하는 방법 트리 순회를 2번 이용하는 방법 동적 계획법을 통해 지름을 구하는 과정은 상당히 직관적이고 쉽다. 하지만 구현이 조금 힘들 수 있다. 그래서 대부분의 사람들은 이보다 단순한 트리 순회 알고리즘을 이용한다. 그런데 이것은 생각보다 이해하기가 어렵다. 게다가 가중치 트리에 대해서도 이 방법이 통하는데 이것까지 아울러서 이해하려면 상당히 힘들다. 그래서 나는 이를 이해하기 위해 트리를 독특한 방식으로 재배치하였다. 동그랗게 생겼으면서 색이 칠해진 것들이 트리의 노드이고, 실선들이 엣지이다. 하얀색 동그라미는 열린 구간임을 나타내는 표시이다. (물론 트리의 지름이 유일하지 않은 경우 하얀색 동그라미 자리에 지름의 한 끝점이 위치할..