그래프에 관하여 1: DFS 트리

이 블로그의 "그래프에 관하여" 시리즈의 첫 번째 카테고리, ❮DFS 트리❯의 개요이다.

DFS 트리는 DFS를 응용한 다양한 알고리즘들을 이해하기 위한 좋은 표현법이자 도구이다. 조금 어려운 감이 있지만 꼼꼼히 이해한다면 큰 도움이 될 것이라고 생각한다.

 

DFS 트리/포레스트란?

어떤 연결 그래프에서 DFS 순회하는 과정을 그렸을 때 나타나는 유향 신장 트리(directed spanning tree)를 DFS 트리라고 한다. 당연히 여러 개가 존재할 수 있다. 연결 그래프가 아닐 경우에는 각 연결 컴포넌트마다 DFS 트리를 만들 수 있으니 DFS 포레스트로 확장해서 생각할 수 있다.

 

유향 그래프의 DFS 트리

 

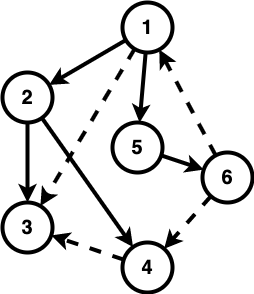
유향 그래프일 경우, DFS 트리의 간선들을 네 가지로 분류할 수 있다.

• 트리 간선(tree edge): DFS 트리에 포함되는 간선. 즉, 간선이 가리키는 정점은 이 간선을 통한 방문이 첫 방문이다. $(1,2)$, $(2,3)$, $(2,4)$, $(1,5)$, $(5,6)$
  
• 순방향 간선(forward edge): DFS 트리에 포함되지 않고, 조상→후손 방향인 간선. $(6,1)$
  
• 역방향 간선(back edge): DFS 트리에 포함되지 않고, 후손→조상 방향인 간선. $(6,1)$
  
• 교차 간선(cross edge): 조상-후손 관계가 아닌 간선. 이 간선은 이미 방문이 끝난 다른 서브트리를 향할 것이다. $(4,3)$, $(6,4)$
  

무향 그래프의 DFS 트리

 

무향 그래프일 경우에는 순방향 간선과 교차 간선이 발생하지 않는다. 그저 역방향 간선으로 취급될 뿐이다. 직접 그려보면 쉽게 와닿는다.

DFS 트리를 이용하는 다양한 사례

• [그래프에 관하여 1: DFS 트리] SCC
• 단절점, 단절선과 그 외 확장된 내용을 다룰 생각이지만, 아직 필자가 지식이 부족한 관계로 무기한 보류한다.