[그래프에 관하여 1: DFS 트리] SCC

이 블로그의 "그래프에 관하여" 시리즈의 첫 번째 카테고리, ❮DFS 트리❯에서 다루는 첫 번째 주제이다.

 

편의를 위해 다음 표현을 정의하자.

• 정점 $v$의 방문 시작 시각: $s(v)$
• 정점 $v$의 방문 종료 시각: $f(v)$

SCC란?

어떤 방향 그래프가 모든 정점에 대해, 다른 모든 정점으로 갈 수 있다면 강하게 결합(strongly connected)되었다고 한다.

모든 방향 그래프는 SCC(strongly connected component; 강결합 컴포넌트)로 나눌 수 있다. SCC란 모든 정점에서 다른 모든 정점으로 갈 수 있는 최대 크기의 정점 집합을 의미한다.

세 개의 강결합 컴포넌트로 나뉜 그래프

 

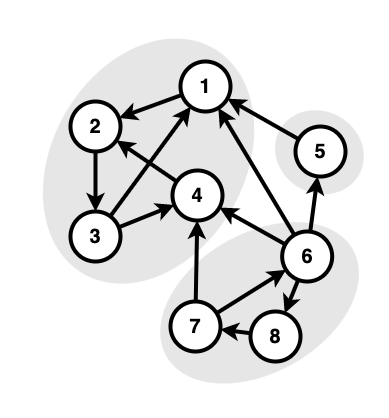
각 SCC를 새로운 정점으로 하고, 그 안의 모든 정점들에서 나가는 간선을 새로운 정점의 간선으로 갖게 하여 컴포넌트 그래프(component graph)를 만들 수 있다. 이 때 이 컴포넌트 그래프는 DAG(directed acyclic graph; 사이클 없는 유향 그래프) 형태를 띠게 된다. 이는 SCC의 정의를 바탕으로 귀류법을 이용해 쉽게 증명할 수 있다.

 

여담으로, 후술할 SCC 알고리즘들의 원리는 Codeforces 레드 코더들도 이해하지 않고 사용하는 경우가 많다고 한다.

Kosaraju's algorithm?

이 알고리즘은 우선 DFS 한 번으로 그래프 $G$의 각 정점의 탐색 종료 시간, $f(v)$를 구해 둔다. 그 다음, $G^T$에서 $f(v)$의 내림차순으로 정점들을 선택하여 DFS를 수행한다. 이렇게 생성된 $G^T$의 DFS 포레스트의 각 DFS 트리들이 그래프 $G^T$의 SCC이다. 이는 정확히 $G$에도 대응되기 때문에 $G$의 SCC이기도 하다.

아무래도 이유가 와닿지 않는다. 그럼 알고리즘이 생성해야 하는 정답인 컴포넌트 그래프는 유일하니까, 알고리즘이 만들어내는 컴포넌트 그래프가 정답과 다르지 않음을 보이자.

 

정당성

정리. $\displaystyle C_1⤳ C_2 \Rightarrow \max_{v\in C_1}f(v)>\max_{v\in C_2}f(v)$

두 SCC $C_1$, $C_2$에 대해 위상 정렬의 방향이 $C_1⤳ C_2$가 된다면, 어떤 SCC의 어떤 정점부터 먼저 DFS를 시작했는지와 무관하게 항상 $\max_{v\in C_1}f(v)>\max_{v\in C_2}f(v)$가 성립한다. 왜 그럴까? $C_1$에서 DFS가 수행되는 상황을 생각하자. 만약 $C_2$가 이미 순회를 끝냈다면, 자명하게 $C_1$의 방문 종료 시각이 더 늦다. 그렇지 않다면, $C_2$를 순회하고 $C_1$에서 끝나기 때문에 역시 $C_1$의 방문 종료 시각이 더 늦다.

한편, $\min$이나 $s(v)$를 이용해 우선 순위를 규정할 수는 없냐고 생각할 수 있다. 직접 경우를 나눠보면 정말로 다른 규칙으로는 우선 순위가 들어맞지 않는다는 것을 확인할 수 있다.

 

보조정리 1. $G^T$의 각 DFS 트리에 서로 다른 SCC의 정점이 포함되지 않는다

$G^T$는 간선이 전부 뒤집혔기 때문에 $f(v)$에 대한 내림차순으로 DFS를 수행하면 컴포넌트 그래프에서 진출 차수(out degree)가 $0$인 정점에 대응되는 컴포넌트들부터 DFS를 수행하는 꼴이 된다.

따라서 수행중인 SCC와 다른 SCC로 연결되는 간선을 타고 나갈 수 있는 상황은 없다. 이미 그 SCC는 수행을 완료했기 때문이다.

 

보조정리 2. $G^T$의 각 DFS 트리에 하나의 SCC의 모든 정점이 전부 포함된다

같은 SCC 속 임의의 두 정점 $u$와 $v$에 대해, $v$에서 $u$로 가는 경로가 존재한다. 따라서 모든 간선이 뒤집힌 $G^T$에서 $u$에서 $v$로 이동 가능하다.

따라서 임의의 정점 $u$에서 수행한 DFS는 정점 $u$가 속한 SCC의 모든 정점들을 방문한다.

 

코드

$f(v)$의 내림차순은 직접 정렬할 필요없이 스택을 이용하면 된다.

SCC $c$에 대응되는 컴포넌트 그래프의 정점도 $c$이다.

• $\text{num}:=$ SCC의 개수
• $\text{of}[v]:=$ 정점 $v$가 속한 SCC의 번호
• $\text{in}[c], \text{out}[c]:=$ 컴포넌트 그래프의 정점 $c$의 진입 차수, 진출 차수
• $\text{nodes}[c]:=$ SCC $c$에 속한 정점들
• $\text{cdj}[c]:=$ 컴포넌트 그래프의 정점 $c$의 인접 리스트
• $\text{rdj}[c]:=$ 뒤집힌 그래프의 정점 $c$의 인접 리스트

int n;
vector<int> adj[N];

namespace scc {
    int num, of[N], in[N], out[N];
    vector<int> nodes[N], cdj[N];
    vector<int> rdj[N]; stack<int> stk; bool vis[N];
    void dfs1(int s) {
        if (vis[s]) return;
        vis[s] = true;
        for (auto u : adj[s]) dfs1(u);
        stk.push(s);
    }
    void dfs2(int s) {
        if (vis[s]) return;
        vis[s] = true;
        nodes[of[s] = num].push_back(s);
        for (auto u : rdj[s]) dfs2(u);
    }
    void build() {
        rep(u,1,n) for (auto v : adj[u]) rdj[v].push_back(u);
        rep(u,1,n) dfs1(u);
        fill(vis+1,vis+n+1,0);
        while (not empty(stk)) {
            int u = stk.top(); stk.pop();
            if (not vis[u]) ++num, dfs2(u);
        }
        rep(u,1,n) for (auto v : adj[u]) {
            if (of[u] != of[v]) {
                in[of[v]]++, out[of[u]]++;
                cdj[of[u]].push_back(of[v]);
            }
        }
    }
}

Tarjan's algorithm?

이 알고리즘은 dfs 한 번을 영리하게 수행하여 SCC를 분리해 낸다.

그래프를 탐색하면서 dfs forest가 나오는데, 다른 트리끼리는 같은 SCC에 등장하지 않음이 자명하므로 각 dfs tree에 대해 생각하자.

각 서브트리는, 그 서브트리의 루트에서부터 이동할 수 있다.

그래서 서브트리 속 정점들 중 역간선으로 현재 정점 이상으로 높이 올라갈 수 있다면, SCC로 묶어주는 것을 반복한다.

이 알고리즘의 정당성은 꽤나 직관적이므로 스스로 생각해보길 바란다.

 

코드

SCC $c$에 대응되는 컴포넌트 그래프의 정점도 $c$이다.

• $\text{num}:=$ SCC의 개수
• $\text{of}[v]:=$ 정점 $v$가 속한 SCC의 번호
• $\text{in}[c], \text{out}[c]:=$ 컴포넌트 그래프의 정점 $c$의 진입 차수, 진출 차수
• $\text{nodes}[c]:=$ SCC $c$에 속한 정점들
• $\text{cdj}[c]:=$ 컴포넌트 그래프의 정점 $c$의 인접 리스트
• $\text{ord}[v]:=$ 방문 순서, 즉 $s(v)$
  

int n;
vector<int> adj[N];

namespace scc {
    int num, of[N], in[N], out[N];
    vector<int> nodes[N], cdj[N];
    int t, ord[N]; stack<int> stk;
    int tarjan(int s) {
        if (ord[s]) return of[s] ? 1e9 : ord[s];
        int r = ord[s] = ++t; stk.push(s);
        for (auto u : adj[s]) r = min(r,tarjan(u));
        if (r == ord[s]) {
            ++num; int u;
            do {
                u = stk.top(), stk.pop();
                nodes[of[u] = num].push_back(u);
            } while (u != s);
        }
        return r;
    }
    void build() {
        rep(u,1,n) tarjan(u);
        rep(u,1,n) for (auto v : adj[u]) {
            if (of[u] != of[v]) {
                in[of[v]]++, out[of[u]]++;
                cdj[of[u]].push_back(of[v]);
            }
        }
    }
}

알고리즘 비교

효율성 측면에서 Tarjan's algorithm이 살짝 더 빠르다.

이해의 측면에서 Tarjan's algorithm이 직관적이라고 생각한다.

구현할 때에는 코드 길이 자체는 Kosaraju's algorithm 더 길지만, 로직이 단순해서 더 쉽다고 생각한다.

 

path-based SCC algorithm도 괜찮다고 하는데, 지금 알아볼 생각은 없어서 링크만 걸어둔다.