이 글에서는 구간 트리(segment tree), 펜윅 트리(fenwick tree), 느리게 갱신되는 구간 트리(segment tree with lazy propagation)들이 성립하는 조건을 알아볼 것이다. 다만, 이 글에는 한계가 존재한다. 구간 트리를 하나의 Black-Box(기능은 알지만 작동 원리를 이해할 수 없는 복잡한 기계 장치나 시스템, 물체)로 바라보기 때문에 직사각형들의 합집합의 넓이를 구하는 문제와 같이 구간 트리의 구조를 변형시키는 문제에는 이 글의 내용이 적용이 되지 않을 수 있다. 기본 질의응답의 대상인 배열은 $[a_1,a_2,\ldots,a_n]$이다. 배열 속 원소들을 포함하는 집합 $S$, 원소들 간의 이항 연산 $*$, 갱신 함수의 집합 $F$가 있다. 이때, 당연..

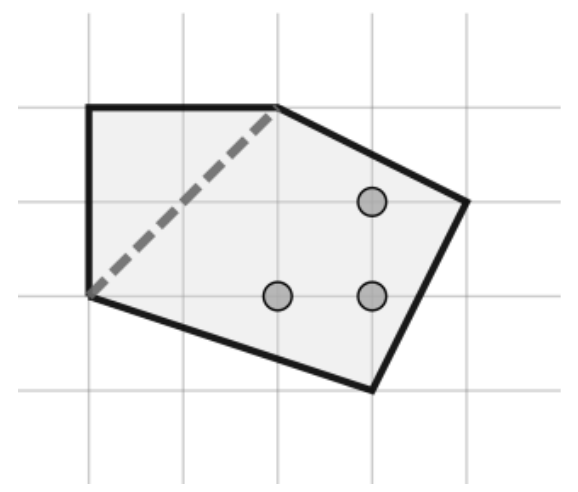
계산기하의 기본 도구들을 소개합니다. 마음가짐 기하 문제는 예외 처리가 적고, 구현이 쉬운 형태의 표현 방법 및 풀이를 이용해야 한다. 그리고 실수 좌표보다는 정수 좌표를 이용해야 한다. 그래서 이 글은 실수를 적극적으로 이용하는 문제는 논외로 한다. 그래서 이중적 의미로 "실수 없는 계산기하"이다. 템플릿 기하를 여행하는 Competitive Programmer를 위한 안내서에서 소개된 편리한 표현 방법을 따른다. 위 글에서 참고한 예외 사항이다: 점이 [1, 2개 / 일직선상 / 위에 존재] 직선, 선분이 [평행 / 일직선상] 중복 존재 점과 벡터 complex을 사용한다. Unspecified Behavior임을 감안하여 몇몇 함수들을 재정의한다. Unspecified Behavior임에도 사용하는..

책 "알고리즘 산책"에서 다음과 같은 내용을 보았다. ...하지만 재귀 호출을 완전히 없애서 함수 호출에 따르는 오버헤드를 피해 보자. 정의 2.1 모든 형식 매개변수를 각각에 상응하는 인자로 사용하는 꼬리 재귀 호출을 순 꼬리 재귀 호출(strictly tail-recursive)이라고 한다. 재귀 호출을 하기 전에 변수의 값을 미리 설정해 주면 순 꼬리 재귀 호출로 고칠 수 있다. int mult_acc3(int r, int n, int a) { if (odd(n)) { r = r+a; if (n == 1) return r; } n = half(n); a = a+a; return mult_acc3(r,n,a); }​ 이제 꼬리 재귀 호출을 while(true) 구문으로 바꾸기만 하면 손쉽게 반복문 형..

*중요: 궁금한건 댓글로 남겨주세요!* int는 32개의 비트의 조합으로 표현된다. signed int의 경우 첫 비트가 부호를 나타내어 $[-2^{31},2^{31})$의 정수를 표현하고, unsigned int의 경우 첫 비트도 일반적인 비트로 사용되어 $[0,2^{32})$의 정수를 표현한다. * 만약 10진수를 2진수로 출력하고 싶다면 cout = 0; --k) cout >k&1); 집합 집합의 표현 정수 $x\in [-2^{31},2^{31})$와 정수 집합 $U=[0,32)$에 대해, $\displaystyle X:=\{k\in U|x\&2^k\neq 0\}$이다. 편의상 $f(x)=X$라고 표기하겠다. 또, $f^{-1}(X)=x$라 하자. 여러가지 집합 $f(0)=\varnothing$, ..

\(lis(i):=A_i\)를 마지막 원소로 갖는 LIS의 길이 \[lis(i)=\max_{j

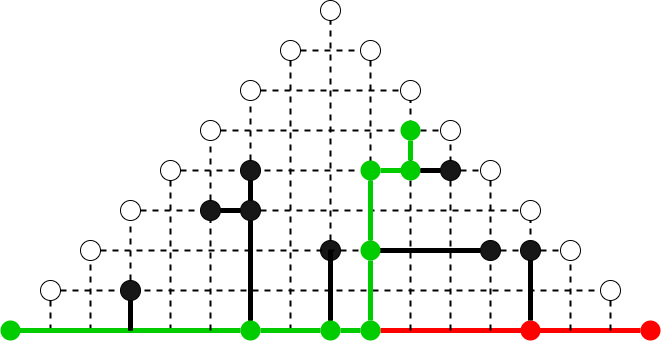
트리의 지름을 구하는 방법은 다음의 몇 가지가 있다. 동적 계획법을 이용하는 방법 트리 순회를 2번 이용하는 방법 동적 계획법을 통해 지름을 구하는 과정은 상당히 직관적이고 쉽다. 하지만 구현이 조금 힘들 수 있다. 그래서 대부분의 사람들은 이보다 단순한 트리 순회 알고리즘을 이용한다. 그런데 이것은 생각보다 이해하기가 어렵다. 게다가 가중치 트리에 대해서도 이 방법이 통하는데 이것까지 아울러서 이해하려면 상당히 힘들다. 그래서 나는 이를 이해하기 위해 트리를 독특한 방식으로 재배치하였다. 동그랗게 생겼으면서 색이 칠해진 것들이 트리의 노드이고, 실선들이 엣지이다. 하얀색 동그라미는 열린 구간임을 나타내는 표시이다. (물론 트리의 지름이 유일하지 않은 경우 하얀색 동그라미 자리에 지름의 한 끝점이 위치할..

https://mathsciforstudent.tistory.com/206?category=919459#toc-%EB%B3%BC%EB%A1%9D%20%EA%BB%8D%EC%A7%88 이 글로 합쳤습니다.