트리의 지름을 구하는 방법은 다음의 몇 가지가 있다.
- 동적 계획법을 이용하는 방법
- 트리 순회를 2번 이용하는 방법
동적 계획법을 통해 지름을 구하는 과정은 상당히 직관적이고 쉽다.
하지만 구현이 조금 힘들 수 있다.
그래서 대부분의 사람들은 이보다 단순한 트리 순회 알고리즘을 이용한다.
그런데 이것은 생각보다 이해하기가 어렵다.
게다가 가중치 트리에 대해서도 이 방법이 통하는데 이것까지 아울러서 이해하려면 상당히 힘들다.
그래서 나는 이를 이해하기 위해 트리를 독특한 방식으로 재배치하였다.
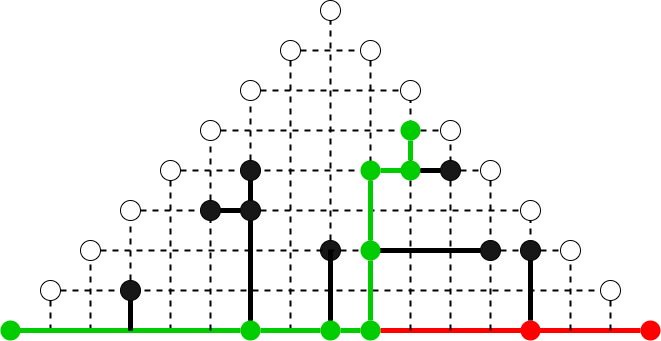
동그랗게 생겼으면서 색이 칠해진 것들이 트리의 노드이고, 실선들이 엣지이다.
하얀색 동그라미는 열린 구간임을 나타내는 표시이다.
(물론 트리의 지름이 유일하지 않은 경우 하얀색 동그라미 자리에 지름의 한 끝점이 위치할 수 있지만, 그렇지 않더라도 원하는 것을 얻어내는 것에는 문제가 없다.)

그림을 부연 설명 하자면,
가운데를 기준으로 가지들은 각각 바깥쪽으로 뻗어나가게 했다.
가지가 3개 이상으로 나뉘는 경우는 뒤에 숨겨졌다고 생각하거나 나선형으로 3차원으로 돌려서 배치했다고 생각해도 무리가 없을 것이다.
그림이 완벽하게 이해가 되었다면, 이 방법으로 원리를 이해해보자.
모든 가지들은 잘 펴서 지름의 위에 올려놓을 수 있다.
하지만 그 어떤 가지들도 지름의 길이를 넘을 수 없다.
따라서 임의의 정점을 기준으로 트리 순회를 진행하는 것은 트리의 지름을 찾는 정당한 방법임이 증명된다.

+) 한 알고리즘 채팅방에서 음수 간선이 존재하는 트리의 지름을 찾을 때도 정당한가라는 Topic이 나왔는데,
반례를 찾음으로서
음수 간선 트리에서는 안 먹힌다는 사실 또한 알아냈습니다.
'알고리즘 설명 > 기타' 카테고리의 다른 글
| 실수 없는 계산기하(1) ★ (0) | 2022.02.17 |
|---|---|
| 두 포인터 구현 바로잡기 ★ (0) | 2022.02.01 |
| 비트 ★ (1) | 2022.01.21 |
| LIS의 최적화 (6) | 2021.02.02 |
| 볼록껍질 (Convex Hull) (0) | 2021.01.21 |