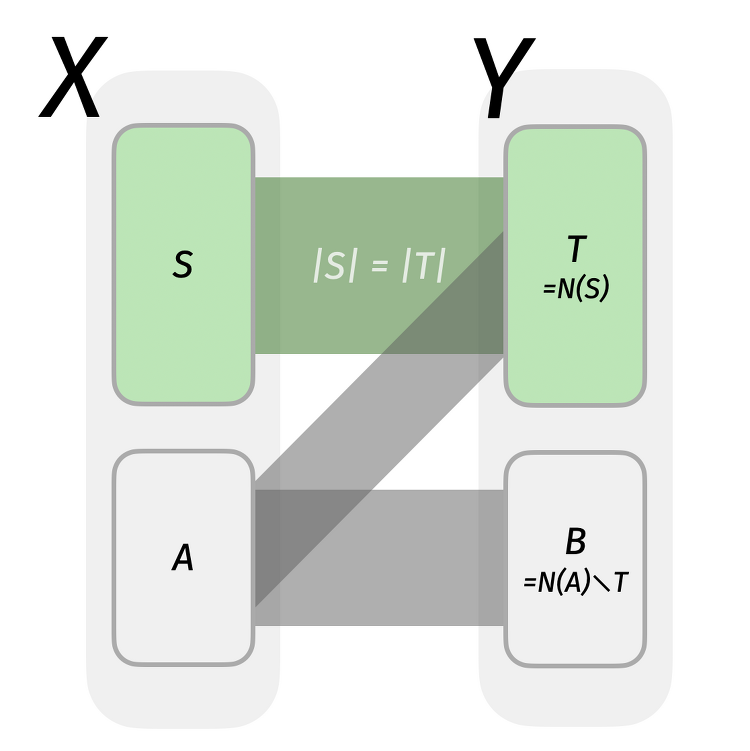
홀의 정리는 홀의 결혼 정리라고도 불리우는 정리로, 이분 매칭에서 유용하게 쓰이거나 다른 그래프 이론의 다양한 정리들의 증명에 도움이 된다. 홀의 정리를 증명해 보았다. 그냥 검색해봐도 되지만, 홀의 정리 문제 상황과 유사한 구조에서 비슷한 논리를 이끌어내는 문제가 존재하기 때문에 이를 대비하기 위해서 별도의 특수한 도구 없이 증명하는 것을 목표로 잡았다. Theorem: $($모든 $S\subset X$에 대해 $|S|\le |N(S)|$를 만족$) \iff (\exists X$에서 $Y$로의 완전 매칭$)$ $[\Leftarrow]$는 자명한 명제이므로, $[\Rightarrow]$만 증명한다. 좌변의 조건을 "홀의 조건"이라고 부르자. 수학적 귀납법으로 접근해 보자. $|X|$의 크기에 대한 귀납법..

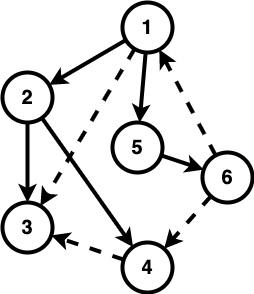
이 블로그의 "그래프에 관하여" 시리즈의 첫 번째 카테고리, ❮DFS 트리❯의 개요이다. DFS 트리는 DFS를 응용한 다양한 알고리즘들을 이해하기 위한 좋은 표현법이자 도구이다. 조금 어려운 감이 있지만 꼼꼼히 이해한다면 큰 도움이 될 것이라고 생각한다. DFS 트리/포레스트란? 어떤 연결 그래프에서 DFS 순회하는 과정을 그렸을 때 나타나는 유향 신장 트리(directed spanning tree)를 DFS 트리라고 한다. 당연히 여러 개가 존재할 수 있다. 연결 그래프가 아닐 경우에는 각 연결 컴포넌트마다 DFS 트리를 만들 수 있으니 DFS 포레스트로 확장해서 생각할 수 있다. 유향 그래프일 경우, DFS 트리의 간선들을 네 가지로 분류할 수 있다. 트리 간선(tree edge): DFS 트리에 ..

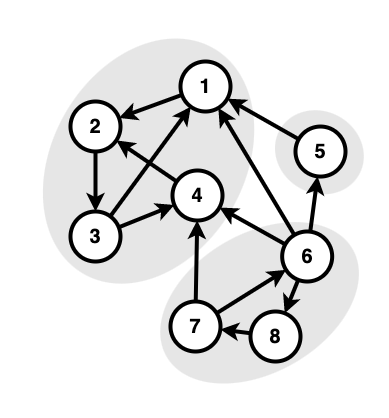
이 블로그의 "그래프에 관하여" 시리즈의 첫 번째 카테고리, ❮DFS 트리❯에서 다루는 첫 번째 주제이다. 편의를 위해 다음 표현을 정의하자. 정점 $v$의 방문 시작 시각: $s(v)$ 정점 $v$의 방문 종료 시각: $f(v)$ SCC란? 어떤 방향 그래프가 모든 정점에 대해, 다른 모든 정점으로 갈 수 있다면 강하게 결합(strongly connected)되었다고 한다. 모든 방향 그래프는 SCC(strongly connected component; 강결합 컴포넌트)로 나눌 수 있다. SCC란 모든 정점에서 다른 모든 정점으로 갈 수 있는 최대 크기의 정점 집합을 의미한다. 각 SCC를 새로운 정점으로 하고, 그 안의 모든 정점들에서 나가는 간선을 새로운 정점의 간선으로 갖게 하여 컴포넌트 그래프(..