홀의 정리 (Hall's theorem)

홀의 정리는 홀의 결혼 정리라고도 불리우는 정리로, 이분 매칭에서 유용하게 쓰이거나 다른 그래프 이론의 다양한 정리들의 증명에 도움이 된다.
 
홀의 정리를 증명해 보았다. 그냥 검색해봐도 되지만, 홀의 정리 문제 상황과 유사한 구조에서 비슷한 논리를 이끌어내는 문제가 존재하기 때문에 이를 대비하기 위해서 별도의 특수한 도구 없이 증명하는 것을 목표로 잡았다.
 
Theorem: $($모든 $S\subset X$에 대해 $|S|\le |N(S)|$를 만족$) \iff (\exists X$에서 $Y$로의 완전 매칭$)$
 
$[\Leftarrow]$는 자명한 명제이므로, $[\Rightarrow]$만 증명한다. 좌변의 조건을 "홀의 조건"이라고 부르자.
 
수학적 귀납법으로 접근해 보자. $|X|$의 크기에 대한 귀납법으로 잡는 것이 적당할 것이다. 그런데 뭔가 상향식으로 접근이 잘 안 된다. 그러니 관점을 바꿔 하향식 느낌으로, 현재 $(X,Y)$를 이보다 작은 $(X',Y')$에 대한 문제로 축소할 수 있음을 보이는 식으로 접근하자.
 
증명의 어려움이 어디서 비롯되는가?

1. '모든 ~에 대해서'는 통제하기 어려운 조건이다.
2. $X$에서 $S$를 우선적으로 매칭시킬 때:
   • $N(S)$ 중에서 어떤 $|S|$개의 원소들이 매칭되는지 명확하지 않고,
   • 매칭되지 않은 모든 정점들이 여전히 홀의 조건을 만족시킬 수 있는지 불분명하다. ($N(\cdot)$ 자체가 처음과 달라지기 때문)

어려움 1 해소하기:
'모든 ~에 대해서'를 자꾸 조건으로서 의식하지 말고, 그냥 지금 그래프의 상태라고 생각하면 편하다. 목표는 완전 매칭이다.
 
어려움 2 해소하기:
$|S|=|N(S)|$인 경우를 상상해 보자. 완전 매칭을 목표로 하는 이상,
$N(S)$의 원소들은 $S$에 의해 남김없이 매칭되어야 한다. 이것은 $(X,Y)$를 $(X',Y')$으로 줄이는 데 도움이 될 것이다. 왜냐하면 $(X',Y')$이 $(X\setminus S,Y\setminus N(S))$로 특정되기 때문이다. (물론 간선 집합도 같이 축소됨)
 
그럼 반대로, $|S|<|N(S)|$인 경우도 상상해 보자. 사실 $|S|<|N(S)|$인 $S$는 흔할 것이고 별다른 인사이트를 제공하지 않는다. 그러니 조금 더 강한 상태, $S: \forall A\subset S\to |A|<|N(A)|$를 생각해 보자. 이 상황은 꽤나 널널해서, 임의의 $u\in S$를 잡아 임의의 $v\in N(S)$에 매칭시켜도 $(S\setminus \{u\}, N(S)\setminus \{v\})$가 홀의 조건을 여전히 만족한다. 또한, 상태의 크기가 줄어들어 귀납법을 적용하기에도 유리하다. $\color{Red}{(*)}$
 
이 두 가지 관찰을 잘 써먹어 보자. 증명의 흐름은 대충 이렇게 되면 좋을 것 같다:

• 임의의 집합 $|A|<|S|$에 대해 홀의 조건을 만족하는 임의의 $(A,B)$에 대해 $[\Rightarrow]$가 만족한다고 가정
• $|S|=|N(S)|$를 만족하는 어떤 $S\ (\neq \varnothing)$를 찾아내기
  • $S$를 $N(S)$에 남김없이 매칭 (귀납적으로 가능)
  • $(X',Y')$가 홀의 조건을 만족 $\color{Blue}{(*)}$
  • $(X,Y) \leftarrow (X',Y')$ (이후는 귀납적으로 가능)
• 없다면, $(X,Y) \leftarrow (X',Y')$ 이후 귀납적으로 가능 $\color{Red}{(*)}$

 
 
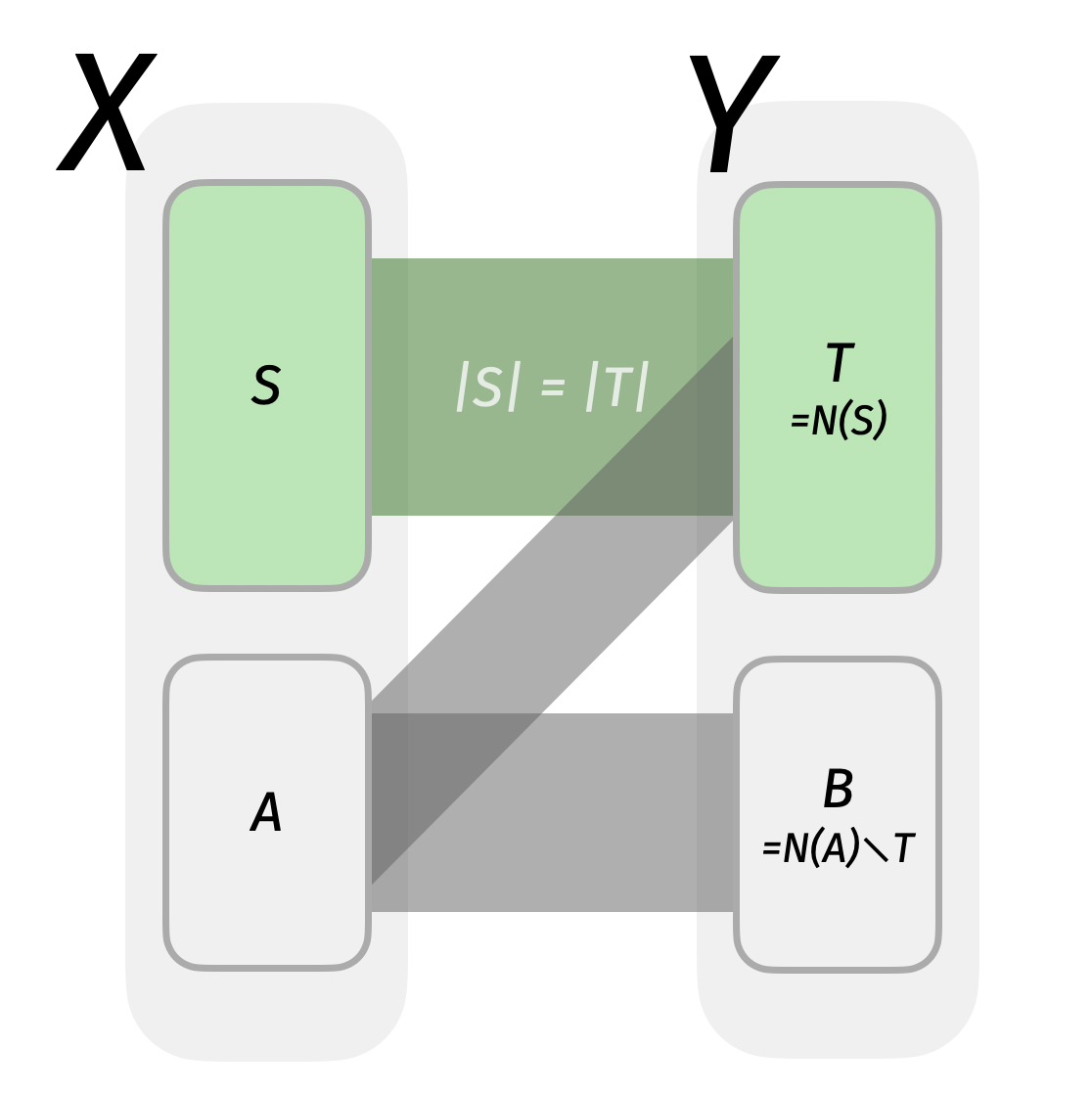
$\color{Blue}{(*)}$가 참임을 증명하자.
 
Claim: $|S|=|N(S)|$를 만족하는 $S$와, $S$에 서로소인 $A$에 대해, $|A|\le |B|$

• $|S|+|A| \le |T|+|B|$
• $|S|=|T|$

$\therefore |A|\le |B|$
$\square$
 
 
이 방법 외에도 증명 방식은 다양하다. 잘 알려진 '그' 이분 매칭 알고리즘이 항상 최대 매칭을 찾는다는 논리로 접근할 수도 있고, 유량 문제로 변환하여 증명할 수도 있다.