요약
겹치지 않는 구간 $N$개가 주어집니다.
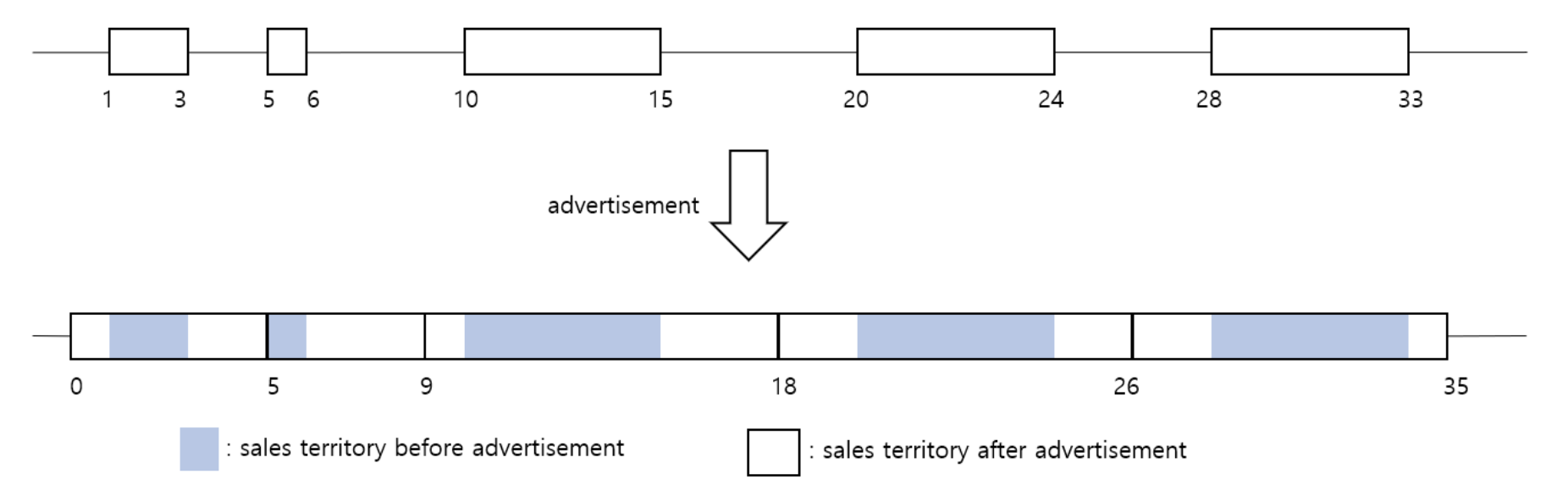
각 구간을 $K$만큼 연장하여 구간 사이사이에 빈틈이 없도록 메꾸고 싶습니다.
그런 $K$를 연속된 구간의 범위을 줄 때마다 찾아서 답하는 문제입니다.
풀이
부분문제 1은 별 의미가 없고, 부분문제 2는 파라매트릭 서치를 하면서 확장영역을 그리디하게 뒷쪽으로 몰아주는 전형적인 방법으로 풀면 됩니다. 이때, 그리디하게 확장영역을 몰아주는 아이디어를 기억해 둡시다.
전체 문제를 풀어봅시다.
$N$이 $3\,000$으로 굉장히 작기 때문에 $O(N^2)$ 전처리를 해두고 매 쿼리에 $O(1)$으로 답하는 것이 가능합니다.
...이제 그 방법을 고민해 봅시다!
관찰 1. 구간 두 개를 두고 간격이 $2K$ 넘게 벌어지면 이 $K$는 불가능하다.
당연히 관찰할 수 있는 사실입니다. 이제 이 관찰을 좀 더 확장해 봅시다.
관찰 2. 구간 $M$개를 두고 간격의 총합이 $MK$ 넘게 벌어지면 이 $K$는 불가능하다.
여기까지도 관찰 1의 연장으로서 쉽게 알아차릴 수 있습니다.
추측 1. 불가능한 범위라면, 그 안의 어떤 연속한 구간 $M$개에 대해 간격 총합이 $MK$ 넘게 벌어진 경우가 있다.
간단한 증명: 부분문제 2와 비슷한 전략으로, 확장을 몰아주는 아이디어를 사용합니다. 우선 확장영역을 그리디하게 뒷쪽으로 몰아줍시다. 그러다 덮지 못하는 첫 빈틈을 잡아서, 그 뒷쪽에는 전부 그리디하게 앞쪽으로 몰아주는 전략을 취합시다. 마지막으로, 빈틈을 덮고도 확장길이가 남는 곳들을 전부 쳐냅니다.

그러고 나면 확장길이가 남는 곳이 없는 상태에서 덮지 못하는 부분이 존재하게 됩니다.
따라서 쳐낸 뒤의 구간 $M$개를 잡으면 간격 총합이 $MK$ 넘게 벌어지므로 추측은 참입니다.
추측의 대우 명제를 생각해 봅시다. 추측인 [불가능 → $MK$ 넘게 벌어진 임의의 연속 부분이 존재]의 대우 명제는 [어떤 구간도 $MK$ 넘게 벌어지지 않음 → 가능]입니다. 그렇다면 모든 부분 구간에 대해 최소의 $K$값을 구하여 DP 전이를 통해 $O(N^2)$에 테이블 전체를 채우면 문제를 해결할 수 있습니다!
UPD - 증명을 같은 논리이지만, 조금 더 단순명료하게 표현할 수 있을 것 같습니다. 부분 구간의 크기에 대한 수학적 귀납법을 세우고, 위 그림처럼 남는 곳의 존재 여부를 갖고 문제를 축소시킬 수 있습니다. 예를 들어 $\ell,\ldots,r-1,r$를 보고 있다면 $\ell,\ldots,r-1$ 선에서는 모든 조건이 잘 성립합니다. 부분 구간의 크기가 지금 보고 있는 것보다 작으니까요. 그럼 $\ell,\ldots,r-1$ 안에서 남는 곳이 있다면, 그 부분을 기점으로 왼쪽은 전부 잘라내면 작은 문제로 축소됩니다. 남는 곳이 없다면 부등식과 그대로 마주하게 되니까 이 부분도 쉽게 증명됩니다. 홀의 정리를 귀납적으로 증명하는 방법을 최근에 적었는데, 이것과 흡사한 면이 있습니다. $|S|<|N(S)|$는 남는 곳이 있는 경우, $|S|=|N(S)|$는 남는 것이 없는 경우와 잘 부합합니다.
#include <bits/stdc++.h>
#define rep(i,a,b) for (auto i = (a); i <= (b); ++i)
#define Mup(x,y) x = max(x,y)
#define mup(x,y) x = min(x,y)
using namespace std;
using ll = long long;
using ii = pair<int,int>;
const ll ceil(ll x, ll y) {
if (x <= 0) return x/y;
return (x-1)/y+1;
}
const int N = 5003, Q = 1e6+3;
int n, q;
int l[N], r[N];
int dp[N][N];
int main() {
scanf("%d%d", &n, &q);
rep(i,1,n) scanf("%d%d", &l[i], &r[i]);
rep(i,1,n) {
dp[i][i] = 0;
int p = 0, mx = 0;
rep(j,i+1,n) {
p += l[j]-r[j-1];
dp[i][j] = ceil(p,j-i+1);
}
}
rep(k,1,n-1) {
rep(i,1,n) {
if (i+k-1 <= n)
Mup(dp[i][i+k],dp[i][i+k-1]);
if (i+k <= n)
Mup(dp[i][i+k],dp[i+1][i+k]);
}
}
rep(i,1,q) {
int s, e;
scanf("%d%d", &s, &e);
printf("%d\n", dp[s][e]);
}
}'PS 문제들' 카테고리의 다른 글
| [IOI 2022 Day 0] Magic Cards (BOJ 25434) ★ (0) | 2023.08.16 |
|---|---|
| [IOI 2011 Day 2] Parrots (BOJ 20137) (0) | 2023.07.29 |
| [KTSC 2023 #1] 던전 (BOJ 27508) (0) | 2023.03.15 |
| [KTSC 2023 #2] 기지 간소화 (BOJ 27605) ★ (0) | 2023.03.15 |
| [POI 03/04 Stage 1] Strings(트리 모델 만들기) (BOJ 1839) (0) | 2023.02.10 |
