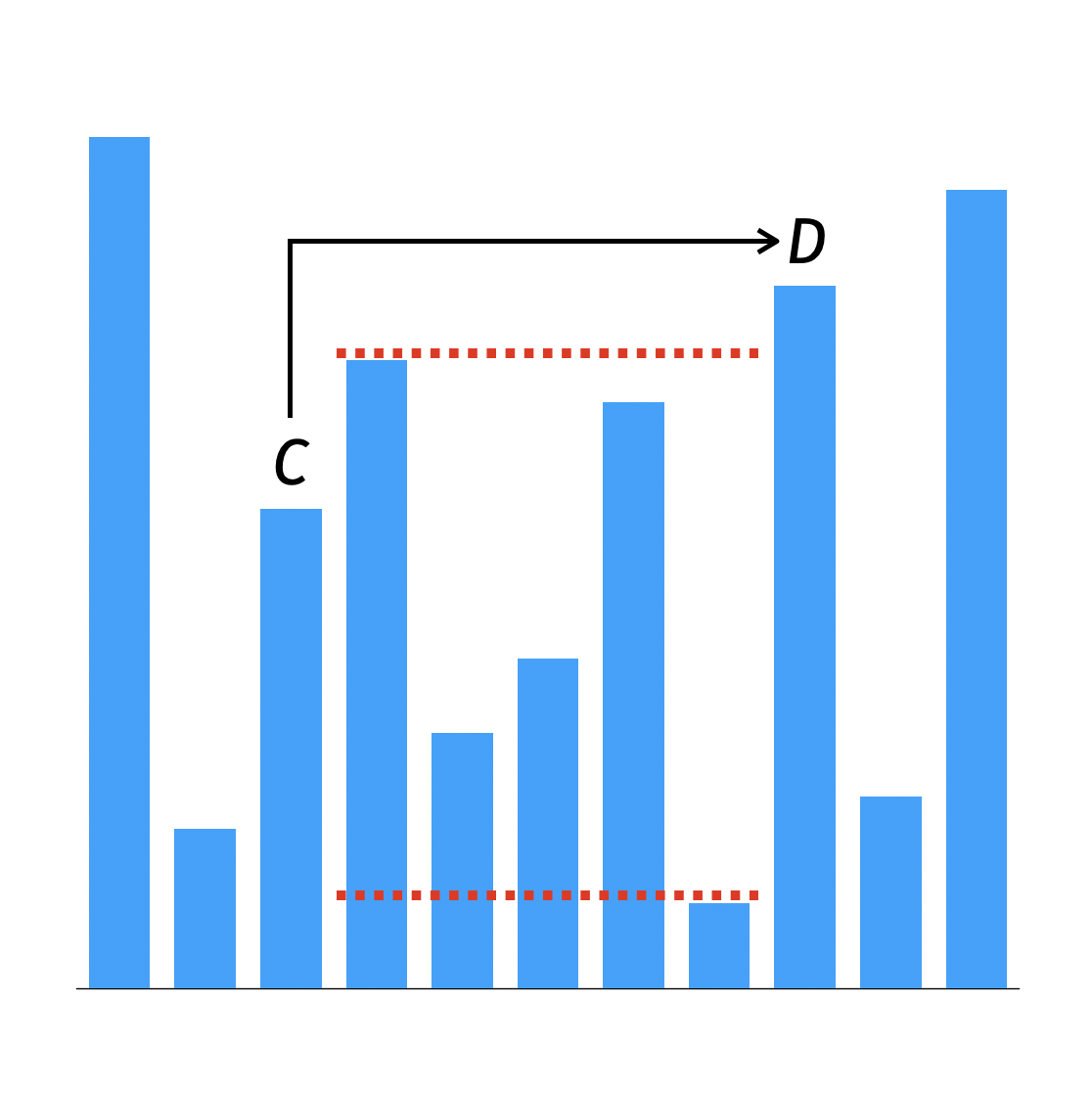
굉장히 재밌는 문제입니다.
부분문제 1 ~ 4
- 부분문제 1 : $C-B$를 반환하면 됩니다.
- 부분문제 2~4 : 그래프로 모델링하여 해결할 수 있습니다.
- 인접한 두 방향의 이동을 스택을 이용해 표현할 수 있고, 이로써 그래프를 만들어 둘 수 있습니다.
- 쿼리마다 multisoure BFS를 해주면 쉽게 답을 구할 수 있습니다.
부분문제 5
- 다시 표현하면 $[B,B]$에서 $[C,C]$로 가는 최단 경로를 찾거나, 도달 불가능함을 판별하는 문제입니다.
- $[A,B]$와 $[C,D]$에 대한 문제의 약한 버전이어서, 확실히 해결하면 정해로 직결될 법한 느낌이 나는 부분문제입니다.
관찰 1. $H_B < H_C$는 '도달 가능'의 필요조건입니다.
- 높이는 이동하는 과정에서 항상 엄격하게 높아지기 때문입니다.

관찰 2. $B$에서 $C$로 이동할 때 $\max_{i\in (B,C)} H_i$ 이상의 높이를 거쳐서 이동합니다.
- $(B,C)$가 높이의 허들로서 작용한다고 생각하면 됩니다.
- 따라서, 도달 가능하기 위해서는 $\max_{i\in (B,C)} H_i < H_C$를 만족해야 합니다.
정리 1. $\max_{i\in [B,C)} H_i < H_C \iff$ '$B$에서 $C$로 도달 가능'
- $[\Leftarrow]$: 앞선 두 관찰에 의해 자명합니다.
- $[\Rightarrow]$: $B$에서 오른쪽으로 이동하기를 반복하면, 언젠가 $C$에 도달할 것이 자명합니다.
- 도달 가능성과 완전히 동치인 명제가 있다는 것은 굉장히 강력한 성질입니다.
생각 1. 도달 불가능한 상황은 즉시 판단하여 걸러낼 수 있으므로, 항상 도달 가능한 상황에서의 최단 경로만 고려하면 됩니다.
- 도달 가능성 판단은 Range maximum query입니다.
생각 2. 왼쪽 이동과 오른쪽 이동 모두 $C$로 도달 가능함을 유지한다면, 한 번에 더 높이 올라가는 것이 이득이지 않을까?


- $X$에서 $Y$로 이동하고 싶은 상황입니다.
- $L$에서 $Y$로도 이동 가능하고, $R$에서 $Y$로도 이동 가능하다면, 둘 중 $H_Y$랑 더 가까운 것을 고르는 것이 이득일 것 같다는 생각이 듭니다.
- 실제로 그렇습니다.
- $H_L>H_R$일 때 $L$로 이동하는 것이 최적인 이유는:
- $R$로 이동한 뒤, 오른쪽으로 이동하기를 반복하여 도달한 $H_L<H_i$인 $i$를 생각하면, 바로 $L$로 이동한 후 $i$로 이동하는 경로가 더 짧거나 같습니다.
- $i$ 도착 이전에 한 번이라도 왼쪽으로 꺾으면 즉시 $L$을 만나므로, 역시 $L$쪽이 최적입니다.
- $H_L<H_R$일 때 $R$로 이동하는 것이 최적인 이유도 마찬가지입니다.
- $L$과 $R$ 사이의 어떤 $i$에 대해서도 $H_L>H_i<H_R$이기 때문에, $L$과 $R$의 위치를 바꾸어도 정확히 같은 상황임을 알 수 있습니다.
생각 3. 왼쪽 이동과 오른쪽 이동 중 $C$로 도달 불가능한 상태가 있다면 어떻게 될까?
- 우선, 오른쪽 이동이 $C$로 도달 불가능한 상태로 이어진다면 [정리 1]에 의해 현재 $C$로 이동하는 것 자체가 불가능합니다.
- 왼쪽 이동이 $C$로 도달 불가능한 상태로 이어진다면, 그리고 오른쪽 이동은 $C$로 도달 가능한 상태로 이어진다면, 이때는 오른쪽 이동을 택하면 됩니다.
생각 4. 정리하면, 도달 가능한 상태를 유지할 때까지 높은 이동을 택하고, 높은 이동을 택할 때 도달 불가능한 시점부터는 오른쪽 이동만 주구장창 택하면 됩니다.
- [생각 3]에서 확인한 바로, 한쪽 이동만 도달 불가능한 경우에, 도달 불가능한 이동은 항상 왼쪽 이동입니다.
- 따라서 $C$에 도달 가능함을 만족할 때 계속 높은 이동을 택하다가 도달 불가능한 상태가 오면 한 번 후진하고 오른쪽 이동만 택하면 됩니다.
- 나아가, 도달 불가능한 최초 시점은 $H_C$보다 높이가 높아지는 최초 시점입니다.
- 만약 오른쪽에서 현재 상태로 왔다면, 애초에 도달 가능성에 모순이 생깁니다.
- 따라서 왼쪽에서 현재 상태로 올 수 밖에 없습니다. 현재 상태가 $i$이고, 직전 상태가 $j$라고 합시다. 직전 상태에서는 도달 가능했으므로 $H_j\le H_C$입니다.
- $\max_{k\in [i,C)} H_k> H_C$이고, $\max_{k\in [j,C)}H_k < H_C$이며, $H_j=\max_{k\in (i,j]} H_k$입니다.
- $\max_{k\in [i,C)} H_k> H_C$이고, $H_j\le \max_{k\in (i,C)}H_k < H_C$입니다.
- 따라서 $H_i > H_C$입니다.
풀이. [생각 4]를 효율적으로 구현
- 높은 이동만 택하는 Sparse table을 구성합니다.
- 오른쪽 이동만 택하는 Sparse table을 구성합니다. 편의상 작은 이동만 택하는 Sparse table을 구성합시다. 오른쪽 이동만 택하는 매 순간은 왼쪽 이동을 할 경우가 $H_C$를 넘어가므로, 오른쪽 이동이 곧 더 작은 이동이기 때문입니다.
- 이진 탐색으로 높은 이동만 택하다가 최초로 $H_C$보다 높이가 높아지는 시점에서 끝냅니다.
- 바로 이전 시점으로 돌아가, 오른쪽 이동만 택하여 $H_C$에 도달하는 시점을 이진 탐색으로 찾습니다.
부분문제 6
- 다시 표현하면 $[A,B]$에서 $[C,C]$로 가는 최단 경로를 찾거나, 도달 불가능함을 판별하는 문제입니다.
- '도달 가능'과 동치 조건은 $(\max_{i\in [B,C)} H_i < H_C) \vee (\max_{i\in [B-1,C)} H_i < H_C) \vee \cdots \vee (\max_{i\in [A,C)} H_i < H_C)$입니다. 정리하면, 여전히 $\max_{i\in [B,C)} H_i < H_C$가 도달 가능 조건임을 알 수 있습니다.
- 부분문제 5와 마찬가지로 도달 불가능한 경우를 걸러내고 도달 가능한 경우만 고려하도록 합시다.
- 단순히 $\max_{i\in [k,C)} H_i < H_C$를 만족하는 $H_k$가 가장 큰 $k$에서 이동을 시작하면 될 것 같습니다.
- $k$의 정의에 따라 $[A,k)$에서는 도달 불가능합니다.
- $(k,B]$에서는 첫 번째 이동을
- $H_i>H_k$이고, $i>B$인 $i$로 할 경우, $k$에서도 똑같이 갈 수 있으므로 여전히 $k$는 최적입니다.
- $H_i<H_k$이고, $i>B$인 $i$로 할 경우, 부분문제 5의 [생각 2]에 의해서 여전히 $k$는 최적입니다.
- $H_i>H_k$이고, $i\le B$인 $i$는 없습니다.
- $H_i<H_k$이고, $i\le B$인 $i$로 할 경우, $(k,i)$를 더미로 치환해서 생각할 수 있고, 최적인 첫 번째 이동은 다시 $k$가 됩니다.
- 따라서 위 생각은 참입니다.
부분문제 7
- 다시 표현하면 $[A,B]$에서 $[C,D]$로 가는 최단 경로를 찾거나, 도달 불가능함을 판별하는 문제입니다.
- $(\max_{i\in [B,C)} H_i < H_C) \vee (\max_{i\in [B,C+1)} H_i < H_{C+1}) \vee \cdots \vee (\max_{i\in [B,D)} H_i < H_D)$가 도달 가능 조건이 되겠습니다.
정리 1. $\max_{i\in [B,C)} H_i < \max_{i\in [C,D] } H_i \iff $ '$[A,B]$에서 $[C,D]$로 도달 가능'
- $[\Rightarrow]$ 높이가 가장 큰 $k\in[C,D]$에 대해,
- $\max_{i\in [B,C)} H_i < H_k$이고, $\max_{i\in [C,k)} H_i < H_k$이므로,
- $\max_{i\in [B,k)} H_i < H_k$입니다.
- 따라서 $[A,B]$에서 $k$로 도달 가능합니다.
- $[\Leftarrow]$ 그렇지 않다고 가정하면,
- 모든 $k\in [C,D]$에 대해 $\max_{i\in [B,k)} H_i > H_k$인 꼴이 됩니다.
- 따라서 $\max_{i\in [B,C)} H_i > H_C$이고, $\max_{i\in [B,C+1)}H_i = \max_{i\in [B,C)}H_i$가 됩니다.
- 결국 귀납적으로, $\max_{i\in [B,k)}H_i = \max_{i\in [B,C)}H_i$가 됩니다.
- 다시 합치면, $\max_{i\in [B,C)} H_i > H_k$가 됩니다. 결국 모순이므로 증명됩니다.
관찰 및 풀이. $[A,B]$에서 $[C,D]$로 도착하기 직전에 찍고 넘어가는 위치 ❌를 다음 세 가지 케이스로 분류할 수 있습니다.
- $B$에서 $[C,D]$로 도달 가능한 경우는 어느 케이스에 넣던 골치가 아파지기 때문에 미리 예외처리 합시다.
- $hurdle=\max_{i\in [B,C)} H_i$이라고 합시다.



- (가) ❌가 $(B,C)$에 존재
- ❌는 정확히 높이가 $hurdle$인 지점이 됩니다.
- $[A,B]$에서 $\max_{i\in [B,C)} H_i$까지의 거리를 구한 뒤 $1$을 더하면 답이 됩니다.
- 존재하면 ❌까지 최단경로에 $1$을 더한 값을 답 후보로 고려합니다.
- 존재하지 않으면 케이스를 무시합니다.
- (나) ❌가 $(A,B)$에 존재
- ❌는 $(A,B)$에서 $hurdle$보다 높은 위치 중 하나가 됩니다.
- 부분문제 6과 같은 논리로, $hurdle$보다 높은 가장 오른쪽 위치에서 $[C,D]$로의 도달 가능성을 판단하는 것으로 충분합니다.
- 존재하면 최단 경로는 $1$이고, 존재하지 않으면 케이스를 무시합니다.
- (다) ❌가 $[0,A)$에 존재
- ❌는 $[0,A)$에서 $hurdle$보다 높은 가장 오른쪽 위치가 됩니다.
- 존재하면 ❌까지 최단경로에 $1$을 더한 값을 답 후보로 고려합니다.
- 존재하지 않으면 케이스를 무시합니다.
- 이때, (가)와 (다)는 한 번에 고려할 수 있습니다.
- (나)에서 최단경로가 $1$인 경우는 걸렀습니다.
- 즉, 고려할 상태에서 $[A,B]$의 모든 높이는 $hurdle$보다 낮습니다.
- 따라서 $[A,B]$에서 가장 높은 위치에서 출발하는 것이 최적입니다.
- $[0,C)$ 안에서 목표 높이를 $hurdle$로 하며 부분문제 5를 푸는 것과 같은 상황입니다.
- 구체적인 위치는 없지만 괜찮습니다. $hurdle$ 미만에서 점프를 하다가 마지막에 $hurdle$로 점프하는 대신 $hurdle$ 이상인 곳으로 점프한다고 생각하면 되기 때문입니다.
- max jump를 하다가 right jump 대신 min jump를 해주어야 합니다. 도착 지점이 오른쪽에 있다는 보장이 없기 때문입니다.
코드.
#include <bits/stdc++.h>
using namespace std;
using vi = vector<int>;
#define rep(i, a, b) for (auto i = (a); i <= (b); ++i)
#define per(i, a, b) for (auto i = (b); i >= (a); --i)
#define siz(x) int((x).size())
const int N = 2e5;
vi adj[N];
int max_jmp[N][20], min_jmp[N][20], lft_jmp[N][20], rgt_jmp[N][20];
int h[N];
void construct_graph(int n, vi &H) {
stack<int> S;
rep(i,0,n-1) {
while (not S.empty() and H[S.top()] < H[i]) S.pop();
if (not S.empty()) adj[i].push_back(S.top());
S.push(i);
}
while (not S.empty()) S.pop();
per(i,0,n-1) {
while (not S.empty() and H[S.top()] < H[i]) S.pop();
if (not S.empty()) adj[i].push_back(S.top());
S.push(i);
}
}
void construct_sparsetable(int n, vi &H) {
rep(i,0,n-1) {
if (adj[i].empty()) {
max_jmp[i][0] = min_jmp[i][0] = lft_jmp[i][0] = rgt_jmp[i][0] = i;
}
else if (siz(adj[i]) == 1) {
max_jmp[i][0] = min_jmp[i][0] = adj[i][0];
lft_jmp[i][0] = adj[i][0] < i ? adj[i][0] : i;
rgt_jmp[i][0] = adj[i][0] > i ? adj[i][0] : i;
}
else if (siz(adj[i]) == 2) {
max_jmp[i][0] = adj[i][0], min_jmp[i][0] = adj[i][1];
if (H[max_jmp[i][0]] < H[min_jmp[i][0]]) swap(max_jmp[i][0],min_jmp[i][0]);
lft_jmp[i][0] = adj[i][0], rgt_jmp[i][0] = adj[i][1];
if (lft_jmp[i][0] > rgt_jmp[i][0]) swap(lft_jmp[i][0],rgt_jmp[i][0]);
}
}
rep(k,1,19) rep(i,0,n-1) {
max_jmp[i][k] = max_jmp[max_jmp[i][k-1]][k-1];
min_jmp[i][k] = min_jmp[min_jmp[i][k-1]][k-1];
lft_jmp[i][k] = lft_jmp[lft_jmp[i][k-1]][k-1];
rgt_jmp[i][k] = rgt_jmp[rgt_jmp[i][k-1]][k-1];
}
}
void init(int N, vi H) {
construct_graph(N, H);
construct_sparsetable(N, H);
rep(i,0,N-1) h[i] = H[i];
}
int Max(int l, int r) {
per(i,0,19) while (l <= lft_jmp[r][i]&&lft_jmp[r][i] < r) r = lft_jmp[r][i];
return h[r];
}
int minimum_jumps(int A, int B, int C, int D) {
if (Max(B,C-1) > Max(C,D)) return -1;
int hurdle = Max(B+1,C-1);
if (h[B] >= hurdle) return 1;
int x = B;
per(i,0,19) while (A <= lft_jmp[x][i]&&lft_jmp[x][i] < x and h[lft_jmp[x][i]] < hurdle) x = lft_jmp[x][i];
{ // Case. (나)
int y = lft_jmp[x][0];
if (A <= y&&y < x) {
y = rgt_jmp[y][0];
if (C <= y&&y <= D) return 1;
}
}
{ // Case. (가)&(다)
int y = x, d = 0, z;
per(i,0,19) while (y < C and h[max_jmp[y][i]] < hurdle) y = max_jmp[y][i], d += 1<<i;
z = rgt_jmp[ max_jmp[y][0] ][0];
if (C <= z&&z <= D) return d+2;
per(i,0,19) while (y < C and h[min_jmp[y][i]] < hurdle) y = min_jmp[y][i], d += 1<<i;
return d+2;
}
}'PS 문제들' 카테고리의 다른 글
| [2022 Yokohama Regional] Make a Loop (BOJ 27421) (3) | 2023.11.08 |
|---|---|
| [NYPC 2022 Round 2-A] 로봇 청소기 ★ (0) | 2023.10.24 |
| [Meta Hacker Cup 2023] C. Wiki Race (2) | 2023.10.22 |
| [IOI 2016 Day 2] Unscrambling a Messy Bug (BOJ 20089) ★ (0) | 2023.09.27 |
| [IOI 2022 Day 0] Magic Cards (BOJ 25434) ★ (0) | 2023.08.16 |