고수들한테 교육적인 문제라고 생각한다.
부분문제 1
- $W_i =0$ $(1 \le i \le N)$
도달 불가능한 경우를 걸러내자.
$H_{i-1} < D_{i}-D_{i-1}$이라면 $i-1$번 기둥에서 $i$번 기둥으로 이동하는 것이 불가능하다. 바닥에 닿기 때문이다.
그런 $i$가 존재하지 않는다면, 항상 $n$번 기둥까지 도달 가능하다.
걸러냈으니, 이제 문제에서 도달 가능함을 전제하고 풀이해 나갈 수 있다.
부분문제 4
- $N \le 500$
- $H_i \le 500$ $(1 \le i \le N)$
- $\mathrm{dp}(i,j):=i$번 기둥의 높이 $j$ 부분까지 이동하는데 걸리는 최소 시간
naive하게 다음과 같은 직관적인 점화식을 짤 수 있다.
$\displaystyle \mathrm{dp}(i,j)=\min \left\{ \min_{D_i-D_{i-1}\le k\le \min(H_{i-1},j+(D_i-D_{i-1}))} \{\mathrm{dp}(i-1,k)+W_i\times (j-k+D_i-D_{i-1}) \}, \min_{\min(H_{i-1},j+(D_i-D_{i-1}))\le k\le \min(H_{i-1},H_i+(D_i-D_{i-1}))} \{\mathrm{dp}(i-1,k)\} \}\right\}$
$O(N\times H^2)$ 시간에 돌아갈 것이다.
그런데 인자가 너무 복잡하다.
인자를 단순화하자.
$i$를 역순으로 보면서 $H_i\leftarrow \min \{ H_i, H_{i+1} + D_{i+1}-D_i \}$로 바꿔줄 수 있다. 즉, 현재 기둥의 높이에서 바로 뛰어서 다음 기둥으로 못 간다면, 고려할 필요가 없는 구간이라는 의미이다. 왜 고려할 필요가 없을까? 한 기둥에서 높이가 높아질 수록 최소 시간이 단조 증가하기 때문이다.
이런 전처리 작업을 거쳤다면, 식은 다음과 같이 변한다.
$\displaystyle \mathrm{dp}(i,j)=\min \left\{ \min_{D_i-D_{i-1}\le k\le j+(D_i-D_{i-1})} \{\mathrm{dp}(i-1,k)+W_i\times (j-k+D_i-D_{i-1}) \}, \min_{j+(D_i-D_{i-1})\le k\le H_{i-1}} \{\mathrm{dp}(i-1,k) \}\right\}$
근데 또 $L$과 $R$이 문제다. 머리가 아프니 맨 앞과 뒤에 Dummy 기둥을 만들어 보자. 맨 앞은 $W_0=0, D_0 = -1, H_0 = D_1+1$로, 맨 뒤는 $W_{n+1}=0, D_{n+1}=D_n+R, H_{n+1}=0$로 설정하자. 이제 초항을 $\mathrm{dp}(0,\cdot)=0$로 설정한 뒤, $\mathrm{dp}(n+1,0)$를 구해주는 문제로 바꿀 수 있다.
결국 시각적으로는 다음과 같은 형태를 갖게 된다.
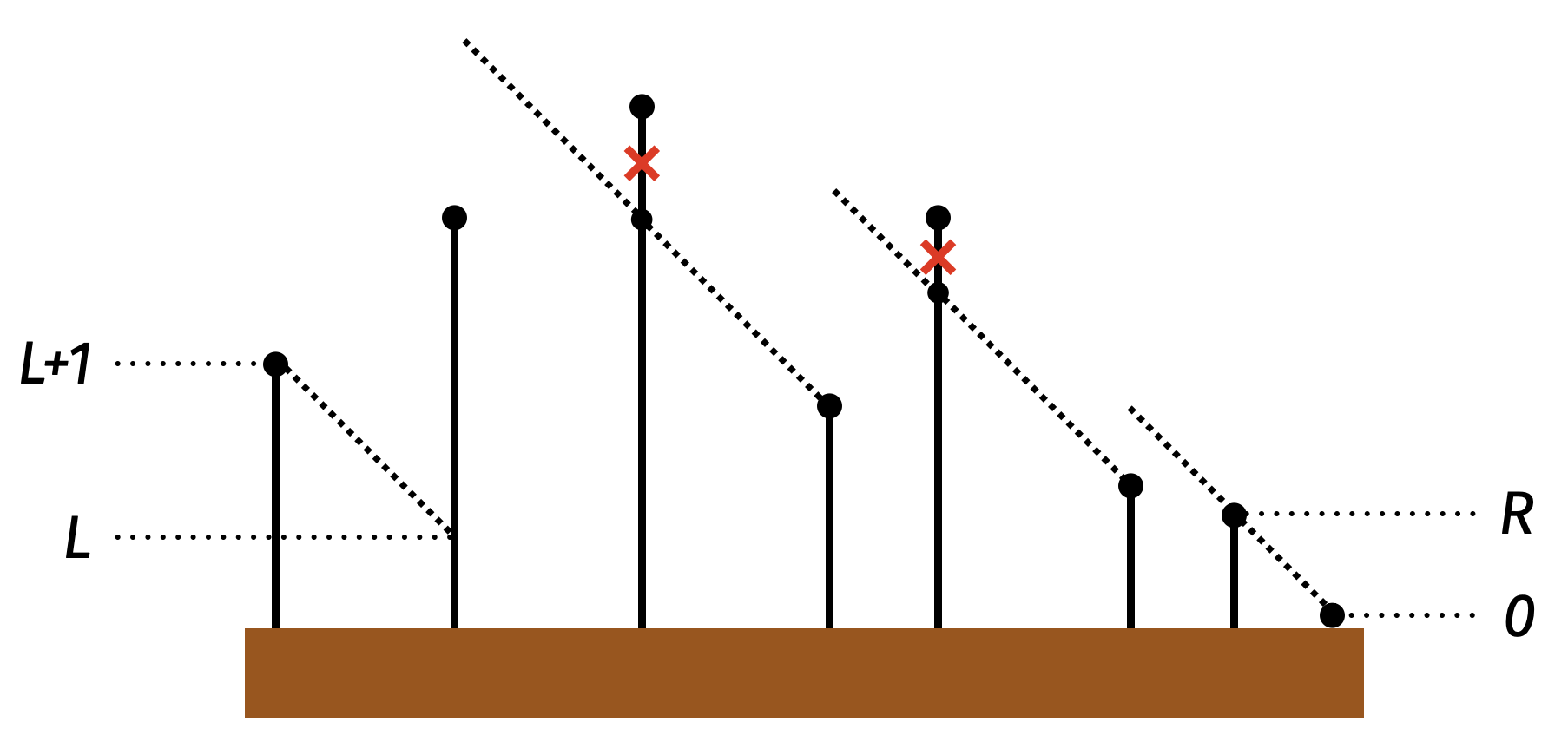
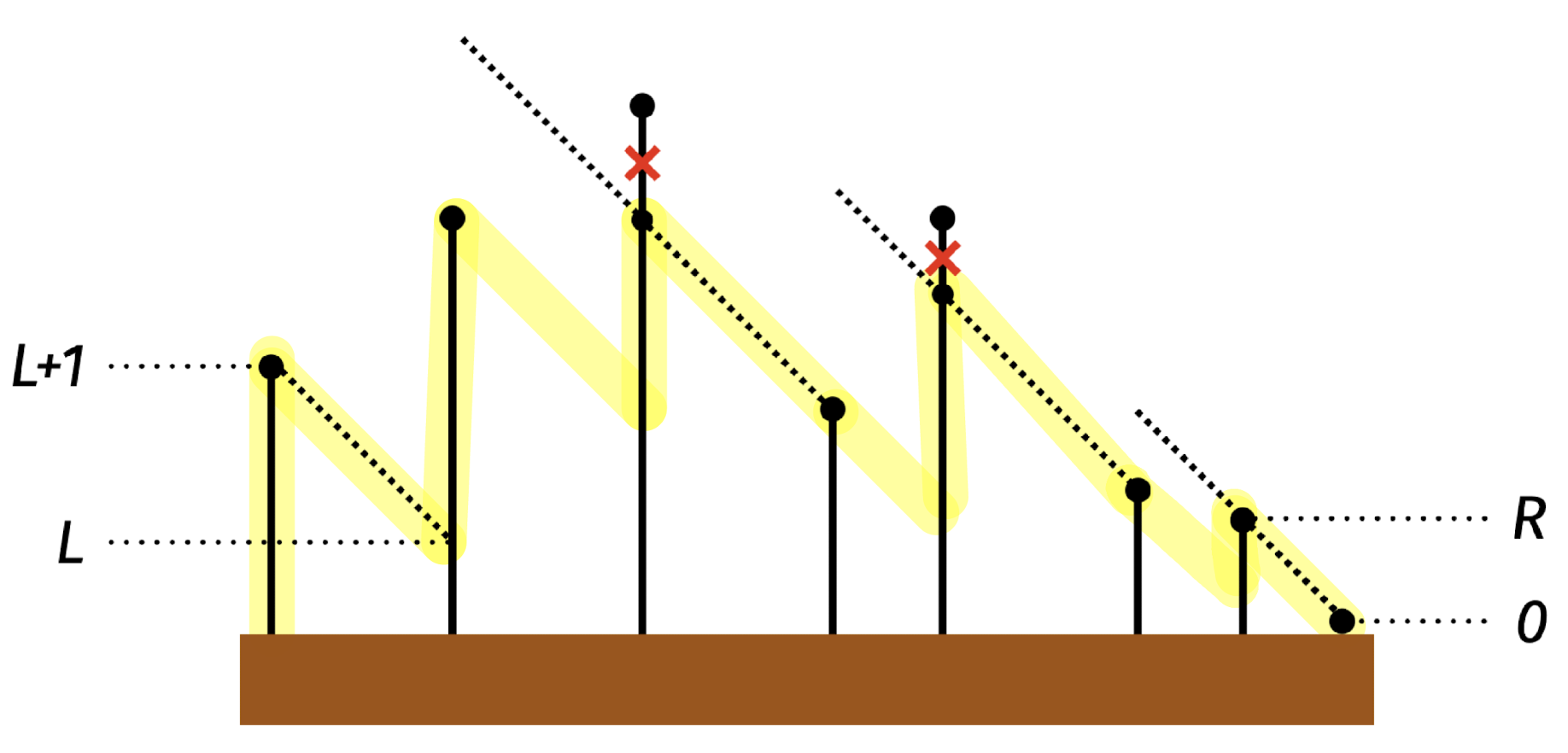
여기서 최대 비용으로 이동하는 범위를 표시해주면, 다음과 같다.
모든 이동은 형광펜 아래, 땅 위에서 일어난다.
부분문제 3
- $W_i \le W_{i+1}$ $(1 \le i \le N-1)$
- $i$번 기둥에서의 상태는 $i-1$번 기둥에서의 상태에 의존한다.
- 각 기둥에서 cost는 높이에 대해 단조성을 갖는다.
- $i-1$번 기둥에서 cost 구조가 $i$번 기둥에서 대부분 유지된다.
- 유지되지 않는, 그러니까 새로 추가되는 부분은 단순한 일차함수 꼴($W_i\times h$)이다.
이쯤되면 무슨 씹덕 알고리즘 두어개가 떠오를만 하다.
"Conex hull trick"과 "Slope trick".
정확히 이 알고리즘이 필요한지는 모르겠지만, 일차함수 꼴 비용 변화에다가 단조성이 있다는 점 등이 유사하니 이 알고리즘들의 핵심적인 아이디어를 고려하며 풀이에 접근하자.
$W_i\le W_{i+1}$이니까, 이전 기둥에서 뛰어서 올 수 있는 범위에서는 cost의 변화가 없어야 최적이다. 이 구간은 $W_{i+1}$로 아무리 기어 올라야, $W_{i}$ 이하인 애들에서 지지고 볶은 것 만 못하기 때문이다.
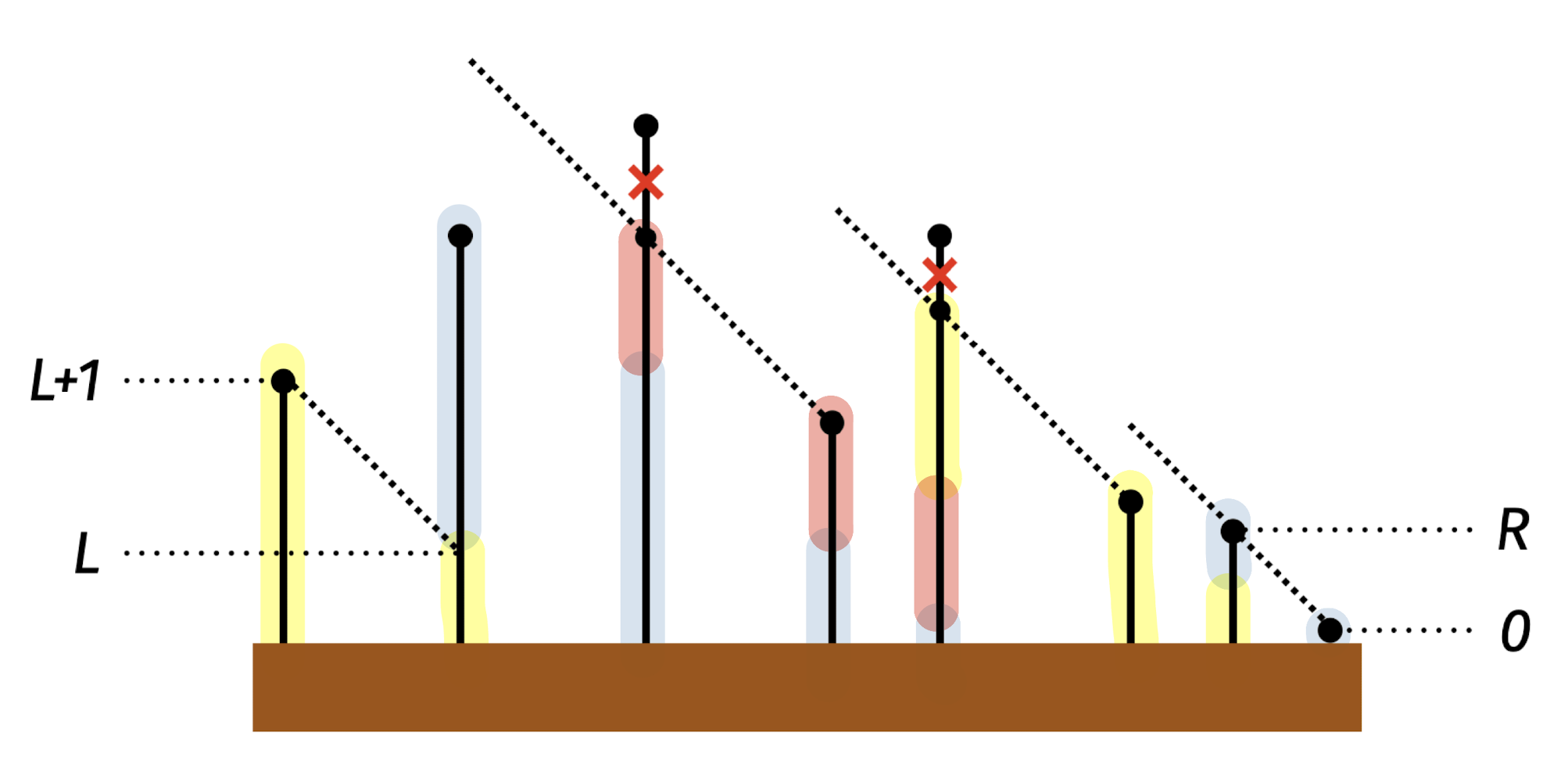
달리 말하면, $W_{i+1}$는 이전 기둥의 최고 높이에서 뛰어 내려온 높이의 '위쪽'만 커버하면 된다는 의미기도 하다.
그림으로 살펴보면, 색깔이 새로 추가되는 부분만 $W_{i+1}$이 커버해주면 된다는 것이다. 그럼 쉽게 풀 수 있다.
부분문제 6
- 추가적인 제약 조건이 없다.
*Slope trick을 알고 있다는 전제 하에 설명한 내용입니다. 모르신다면 "BOJ 수열" 문제를 풀어보세요.
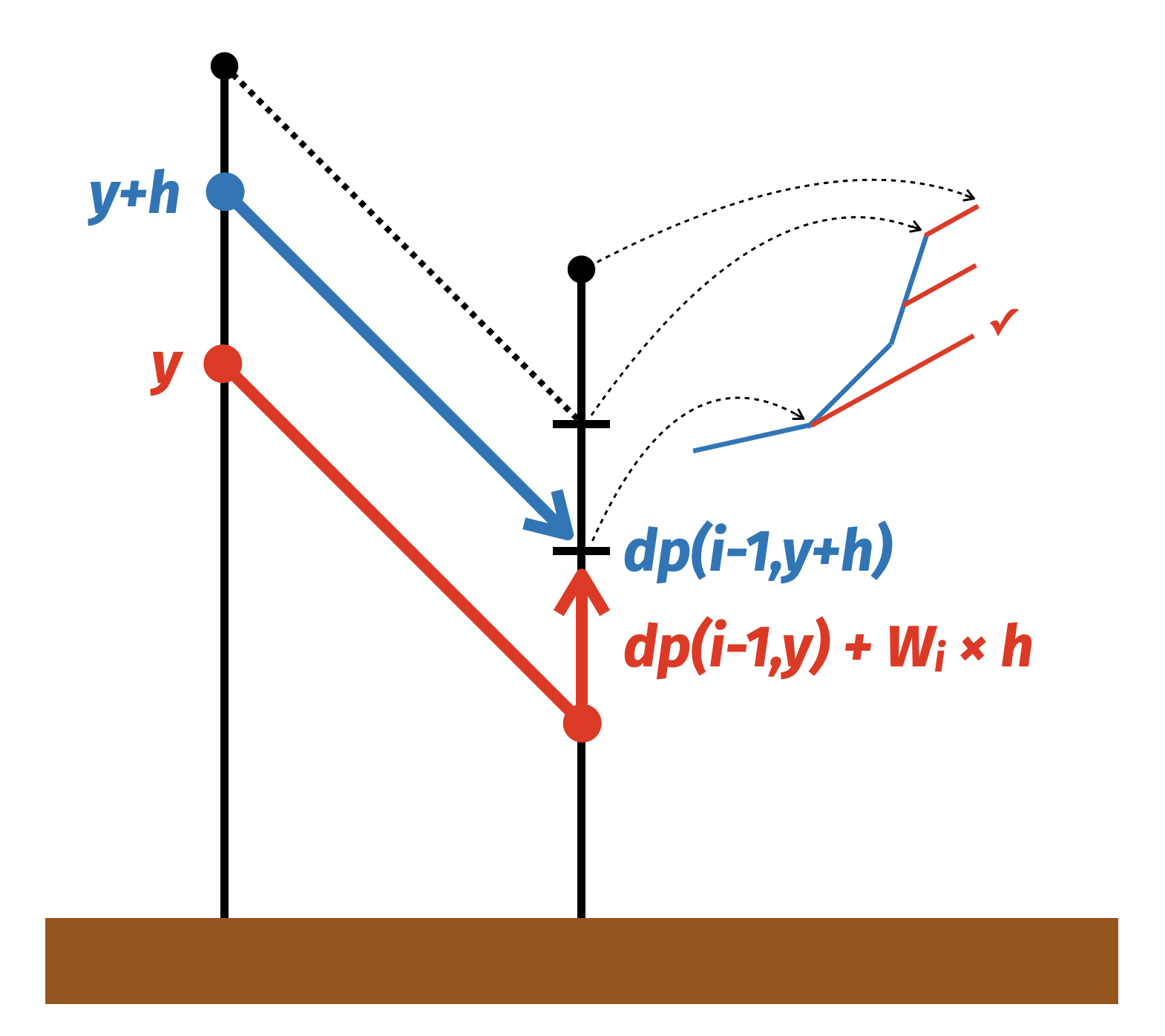
$W_i > W_{i+1}$일 수 있는 상황에서도 크게 다르지 않다. cost 함수에 $W_i$로 커버하는 것이 이득인 구간은 convex 함수가 되도록 $W_i$ 기울기의 새 직선을 끼워넣으면 된다.
이때, 추가하는 각 함수들에 life time이 있다는 것이 문제인데 이것은 deque를 이용하면 된다. deque의 앞쪽에서 life time이 만료된 직선들을 삭제한 후 새로운 직선 추가 작업을 deque의 뒷쪽에 해주면 된다.
덤 1. 좌표축이 평행이동 하는 것은 $D_i$를 더한 값으로 저장함으로써 문제 없이 나타낼 수 있다.
덤 2. 변화량을 갖고 lazy segtree를 이용해 해결할 수도 있겠다.
정답 코드:
#include <bits/stdc++.h>
using namespace std;
using vi = vector<int>;
using ll = long long;
const int N = 5e5+3;
int n;
ll d[N], h[N], w[N];
ll solve() {
deque<array<ll,3>> D;
D.push_back({0,0,d[0]+h[0]});
for (int i = 1; i <= n; ++i) {
while (not empty(D) and D.front()[2] < d[i]) D.pop_front();
ll x = d[i], y = D.front()[0] * x + D.front()[1];
// [d[i],d[i]+h[i]]
while (not empty(D) and D.back()[0] >= w[i]) D.pop_back();
if (not empty(D)) x = D.back()[2], y = D.back()[0]*x+D.back()[1];
ll a = w[i], b = y-a*x, e = d[i]+h[i];
D.push_back({a,b,e});
}
return D.back()[0] * (d[n]+h[n]) + D.back()[1];
}
ll fly(vi D, vi H, vi W, int L, int R) {
n = D.size();
for (int i = 1; i <= n; ++i) {
tie(d[i],h[i],w[i]) = tie(D[i-1],H[i-1],W[i-1]);
if (i > 1 and d[i]-d[i-1] > h[i-1]) return -1;
}
h[0] = L+1, d[0] = -1, w[0] = 0;
++n; h[n] = 0, d[n] = d[n-1]+R, w[n] = 0;
for (int i = n-1; i >= 0; --i) h[i] = min(h[i], h[i+1]+d[i+1]-d[i]);
return solve();
}'PS 기록들' 카테고리의 다른 글
| 11월의 문제들 (0) | 2023.11.08 |
|---|---|
| NYPC 2023 본선 후기 (6) | 2023.10.30 |
| 10월의 문제들 (0) | 2023.10.11 |
| NYPC 2023 Round 2-A & 2-B 후기 (3) | 2023.08.20 |
| [2023 KSAAC Summer / Arena #4] 검수 후기 (3) | 2023.08.20 |

