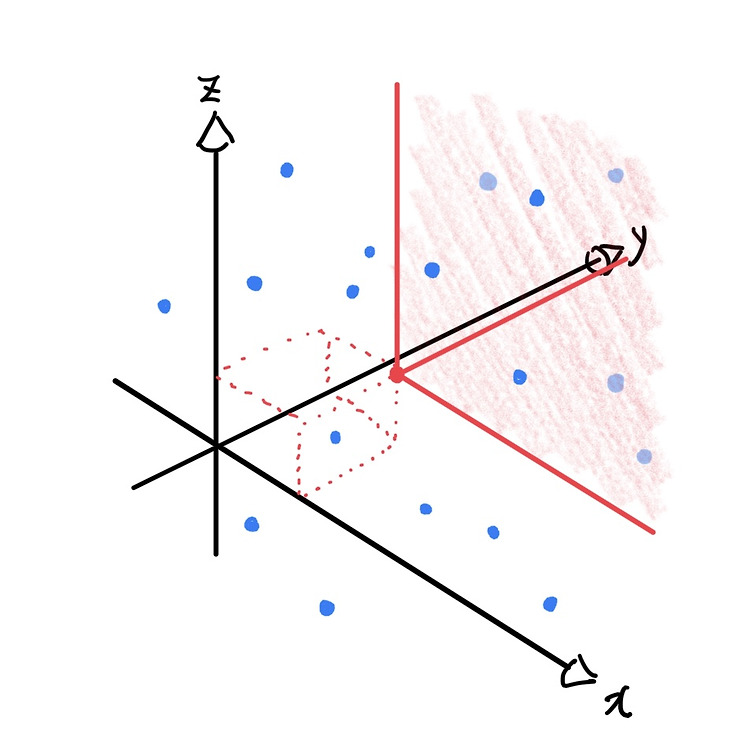
문제 링크 문제에 풀 때 사용할 수 있는 자료구조 테크닉(문제 특성에 비해 약간 오버킬)을 배울 수 있어 좋았다. 또한, 풀이만 6개를 확인했는데... 진짜 이런 고난이도에 조건이 적은 문제는 여러 방법으로 접근할 수 있구나... 싶었다. Subtask: $N ≤ 3\ 000, Q ≤ 3\ 000$ (2점) 더보기 Naive하게 짜면 된다. 2점이라 짜다고 생각했는데 풀고 나니 걸맞는 점수다 ㅋㅋ 코드 Subtask: 점수 $ ≤ 10^5, Z_j =0$ (20점) 더보기 난이도가 확 뛴다. 우선, 각 점수 쌍들을 좌표로서 해석하면 시각화가 되므로 풀이에 접근하기 좋다. 시각화 이후에 간단한 관찰들을 바탕으로 떠오르는 자료구조들이 있을 것이다. 그렇게 다음의 3가지 풀이가 있다: Merge sort tr..
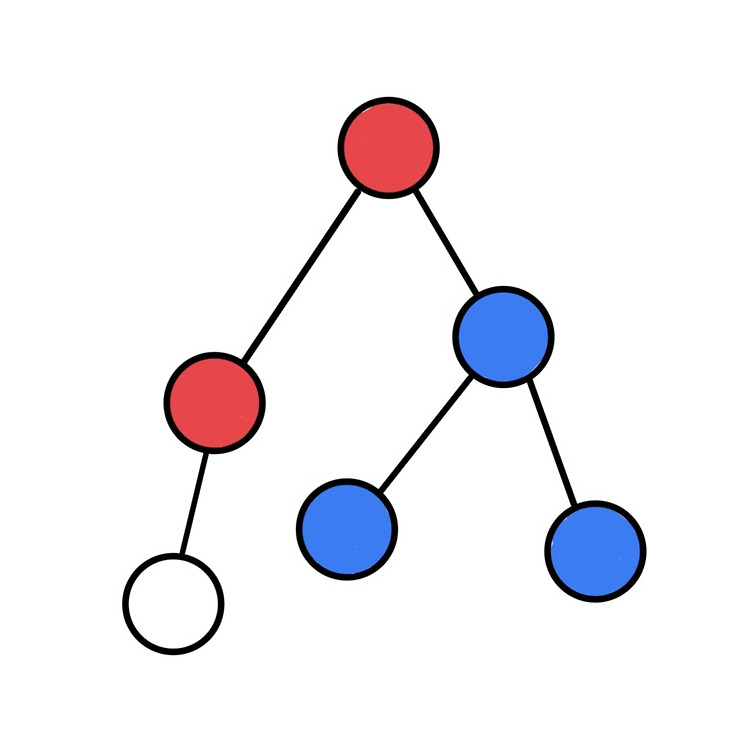
문제 링크재밌는 트리 DP 문제였다.편의상 각 사원 $i$의 실력을 $V_i$, 부모를 $P_i$라고 하자.Subtask: $V_i > 0$ (17점)더보기그냥 최대한 많이 포함하면 이득이다.그런데, 한 팀의 팀장을 전체 트리의 루트로 잡아버리면 다른 팀이 만들어질 수 없다.또한, 루트의 $k$대 독자 후손 노드도 잡아버리면 다른 팀이 만들어질 수 없다. 따라서 1번 노드에서부터 DFS를 돌리다가 처음으로 자식 노드가 2개 이상이 된다면 가장 큰 2개만 골라주면 된다.필자의 코드이다.Subtask: $N\le 5\ 000,\ P_i=i-1$ (12점)더보기직선형 그래프에서 문제를 풀면 된다.Kadane 알고리즘과 꽤 비슷하다.각 노드 $i$마다 $\sum_{i\le k\le j}V_k$가 최대가 되게 하..

5월 중순인데 이제..? 너무 벌레다. 일단, 올해 달성한 것은 USACO Gold, Codeforces Expert이고, 올해 놓친 것은 Google Code Jam 2R 진출, KOI 2차 진출이다. Google Code Jam이야 얼마든 있는 기회인거고... KOI를 2년째 예선 무상으로 지내는 것이 문제다. KOI 예선 무상은 정말 쓰라리고, 생각할수록 침울하다. 당연히 올해는 통과라고 자신했는데, 자신이 무상할 정도로 미친듯이 말아먹었다. 작년에 친 KOI 1차보다 더 조졌다. 하지만, 내가 이걸 계기로 개빡쳐서 PS를 놓을 수 있을까? 답은 '아니오'다. 어차피 재밌어서 하는건데 빡종한다고 다시 안 켤 리가 없다는 것이다. 그런 만큼, KOI 1차에서 내가 저지른 실수들, 잘못된 전략들, 새로..

냐 공통 부분 수열 확장 문제 링크 서브태스크 구성도 좋고, 재미있게 풀었다. 풀이 및 코드 Subtask #1: $|W|=1$(14점) 더보기 자명하다. 왼쪽 확장 경우, 오른쪽 확장 경우로 나눠서 각각 쌍이 존재하는지 확인하면 된다. 하지만 Subtask #2도 충분히 쉬우므로 한번에 긁었다. Subtask #2: $\sum |X|, \sum |Y| \le 300$(17점) 더보기 $W$의 모든 위치에 대해서 문자 $c$를 끼워 넣은 경우에도 여전히 $|X|$와 $|Y|$의 부분 수열이 되는가를 판단하면 된다. 그러면 $\mathcal O(|W|\times |C|\times (|X|+|Y|+|W|))$의 시간이 걸린다. 따라서 대충 $26\times 300^2\approx 2\cdot 10^6$번의 ..

냐 K번째 수 문제 링크 냐 풀이 더보기 사실 루트질 연습하려고 담아둔 문제인데, 그냥 세그트리로 풀었다. 이게 머지 소트 트리 맞나? 아무튼 각 노드가 구간을 커버하는 배열의 정렬된 상태를 담는데... 이렇게 하면 쿼리를 $\mathcal O(\log n)$개의 구간에 대해 각각 $\mathcal O(\log n)$의 이진 탐색을 진행하여서 총 $\mathcal O(\log^2 n)$에 응답할 수 있게 된다. ヘビの JOI 君 문제 링크 풀이 쓰기 좀 귀찮네... 생각을 풀어서 쓰려니 귀찮다. 참고로 이 문제 기여에 나는 #Case_work를 넣었다. 깔끔하게 분류 안 하면 자꾸 꼬이는 듯. 풀이 더보기 물론 다익스트라다. 뭐 다른게 나올 일도 없지 않은가... 그 상태에서 뭘 어떻게 해야되냐가 문제인..

오늘 티어 많이 올린듯 후후 JOI 국가의 행사 문제 링크 3가지 풀이가 존재한다고 한다. 참고 풀이 더보기 멀티소스 다익스트라로 전처리를 해준다. 각 노드 $v$에 대해 구한 최단거리를 $\text{value}[v]$라고 하자. 문제가 $\displaystyle \min _{\text{v}\in \text{경로}} \text{value}[v]$ 쿼리를 푸는 문제로 단순화된다. $\text{value}[v]$의 크기에 따른 크루스칼 변형을 떠올릴 수 있다. 그렇게 구성되는 스패닝 트리 위의 간선을 타는 경로가 최적이다. 따라서 구성된 스패닝 트리로 sparse table을 구성한다. 쿼리를 sparse table로 처리한다. 코드 더보기 구현이 워낙 길어져서, 모듈화시켜서 풀었다. 덕분에 디버깅 없이 1..

냠 굉장한 학생 문제 링크 풀이 더보기 각 학생은 $(a,b,c)$값을 지닌다. 만약 모든 다른 $(a',b',c')$에 대해 $a'>a,\ b'>b,\ c'>c$가 만족한다면 굉장하다. 따라서 $(a,b,c)$를 $a$에 대한 오름차순으로 정렬한 뒤, $\text{RMQ}$ 세그트리에서 $b$번 인덱스에 $c$를 넣는 식으로 관리하면 문제를 풀 수 있다. List of Unique Numbers 문제 링크 $\text{last_pos}[x]$를 관리하면서 풀면 된다. 정사각형 만들기 문제 링크 정확한 내용을 모르겠어서 디코에 질문 올렸다. 풀이 더보기 코드 더보기 #include using namespace std; #define rep(i,a,b) for (auto i=(a); i> n >> m; i..
