지문 링크 / 문제 링크 더보기 이거 풀면서 lazy propagation를 짜는 방식도 바꿨다. 속도가 2배가량 향상되고, 훨씬 직관적으로 변했다. 풀이 더보기 dynamic segment tree + lazy propagation. UPD - 구조체 내부 포인터도 0으로 같이 초기화하지 않으면 컴파일 환경에 따라 UB가 발생할 수 있다! 무조건 다 초기화시키자. 그리고 인덱스로 음수가 들어갈 수 있는 경우 단순한 (s+e)/2는 예상한 대로 동작하지 않는다. 따라서 이 블로그에 있는 "코드 조각들" 글에 있는 floor 함수를 이용해서 나눗셈을 처리하자. #include using namespace std; using ii = pair; using ll = long long; #define rep(i..

문제 링크 플4치고 쉬운? 문제 풀이 더보기 2 3→2 4→3→2 5→2 6→4→3→2 7→2 8→3→2 9→2 10→3→2 주어진 수를 나누지 않는 최솟값 → 어떤 수보다 미만의 모든 수가 주어진 수를 나누게 하는 최솟값 따라서 $$|\{k|(2\nmid k)\}|\times (strength(2)+1)\\+\\ |\{k|(2\mid k)\wedge(3\nmid k)\}|\times (strength(3)+1)\\+\\ |\{k|(2\mid k)\wedge (3\mid k)\wedge (4\nmid k)\}|\times (strength(4)+1)\\+\\ \vdots$$ 를 구해주면 된다. $\mathrm{lcm}$ 단위로 커지기 때문에, 전처리할 $strength(k)$의 종류가 그리 많지 않다는 ..

알고리즘 트레이닝 초록책 2판을 오늘 받아보았다. 새롭게 추가된 내용이 곳곳에 있을 것이기 때문에 앞에서부터 살펴보았다. 역시나 따로 언급되지 않은 '3.3 코드 최적화'라는 목차가 생겼다. 코드 최적화는 고인물들이 아니더라도 통용되고 잘 알려진 기법이다. 하지만, 그 최적화를 깊이있게 이해하는 사람은 드물고, 그냥 입에서 입으로 전해지는 정도인 것 같다. 따라서 최적화의 중요한 부분들을 보충해주는 것이 마음에 들었다. 덕분에 갖고 있던 의문점들도 많이 해결되었다. 컴파일러 출력 컴파일러 최적화 /2, %2 등을 비트연산으로 대체하는 코드들을 보면서 안 예쁘다고 느껴왔었다. 그래서 세그트리 기본문제에다가 비트 연산을 사용한 경우와 그렇지 않은 경우를 비교해 본 바 있다. 하지만 유의미한 속도 차이가 없어..

문제 링크 이 문제를 풀기 전에 BOI의 굉장한 학생을 먼저 풀어보시는 것을 추천드립니다. 풀이 더보기 다익스트라로 $A$로부터의 거리, $B$로부터의 거리, $C$로부터의 거리를 구한 뒤, $A$로부터의 거리의 오름차순으로 $B$로부터의 거리를 좌표압축한 인덱스에 $C$로부터의 거리를 업데이트해주면 된다. #include using namespace std; using ii = pair; using ll = long long; void o_o(){ cerr c >> m; rep(i,1,m) { int x, y, z; cin >> x >> y >> z; adj[x].emplace_back(y,z); adj[y].emplace_back(x,z); } vector v(n); vector bs; ll da[N..

문제 링크 usaco.guide에서 sqrt decomposition 예제로 제일 쉬운거로 추천되어 있었는데, 그걸 왜 곧이곧대로 믿었을까요... 풀 때 사진 참고하세요. 문제 번역 \(1\)부터 \(N\)까지 높이에 대한 내림차순으로 번호가 매겨진 \(N\)개의 마을들이 있습니다.(같은 높이의 마을은 없습니다.) \(M\)개의 운하는 서로 다른 마을을 단방향으로 연결합니다. \(i\)번째 운하(\(1\le i\le M\))은 높은 \(S_i\)에서 낮은 \(E_i\)로 흐릅니다. 운하는 거꾸로 거슬러 올라갈 수 없습니다. 비버 Bitaro의 \(N\)명의 친구들은 \(N\)개의 마을에 살고 있습니다. Bitaro는 \(Q\)번의 파티를 열며, 친구들을 초대할 것입니다. \(j\)번째 파티에는 \(Y_j..

문제 링크 꾸준히 다이아를 풀고 있어서 기쁘다. Subtask: $N≤5\,000$ (40점) 더보기 단순히 $O(n^2)$ LIS를 돌리면 된다. #include using namespace std; using ii = pair; using ll = long long; void o_o(){ cerr > t[i].se.se; } sort(t+1,t+n+1); rep(i,1,n) { lis[i] = 1, cnt[i] = 1; rep(j,1,n-1) { if (t[j].se.fi < t[i].fi.fi and t[j].se.se < t[i].fi.se) { if (lis[i] < lis[j]+1) { lis[i] = lis[j]+1; cnt[i] = cnt[j]; } else if (lis[i] == lis..

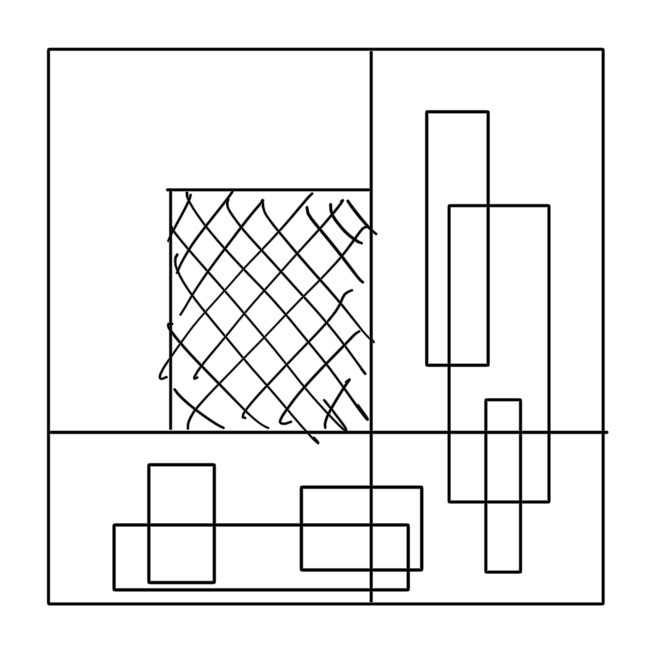
문제 링크 예전 IOI라서 서브태스크가 없다. 플1... 까지는 아닌 것 같다. 풀이 더보기 겹치지 않는 두 직사각형을 선택한다는 조건을 잘 고민해보면, 수직선 하나를 두고 양쪽에서 선택한다는 의미가 된다. 그래서 아래의 색칠된 직사각형이 좌상단 영역에서 둘레가 최소가 되는 조건 만족 직사각형이라면, 저기 여러가지 나머지 직사각형들 중 최소가 되는 것과 함께 고려해주면 된다는 것을 알 수 있다. 따라서, $a(i,j):=(i,j)$를 우하단 점으로 하는 직사각형들 중 최소, $b(i,j)=i\le i',\, j\le j'$일 때, $(i',j')$을 좌상단 점으로 하는 직사각형들 중 최소로 잡고 $\min$ 2D 누적합을 진행해주면 된다. #include using namespace std; using ..

문제 링크 Subtask: $M = 2, 3 ≤ N ≤ 10\,000$ (14점) 더보기 어차피 부분행렬 속 각 열 속의 등수가 전부 같은 것이 조건이므로, 행렬의 각 열의 순서는 바뀌어도 상관이 없다. 따라서 각 열을 첫번째 행의 크기 순서대로 정렬하는 것이 가능한데, 이러면 LIS 문제로 환원되어 쉽게 풀 수 있다. $O(n^2)$으로도 가능한데, $O(n\log n)$으로 풀어 Subtask #3와 함께 긁었다. Subtask: $M = 3, 3 ≤ N ≤ 10\,000$ (9점) 더보기 $O(n\log n)$의 LIS는 적용할 수 없다. 따라서 $O(n^2)$ LIS를 사용하여 풀 수 있다. 코드 Subtask: $M = 2, 3 ≤ N ≤ 2\cdot 10^5$ (15점) 더보기 세그트리를 이용..