재밌는 트리 DP 문제였다.
편의상 각 사원 $i$의 실력을 $V_i$, 부모를 $P_i$라고 하자.
Subtask: $V_i > 0$ (17점)
그냥 최대한 많이 포함하면 이득이다.
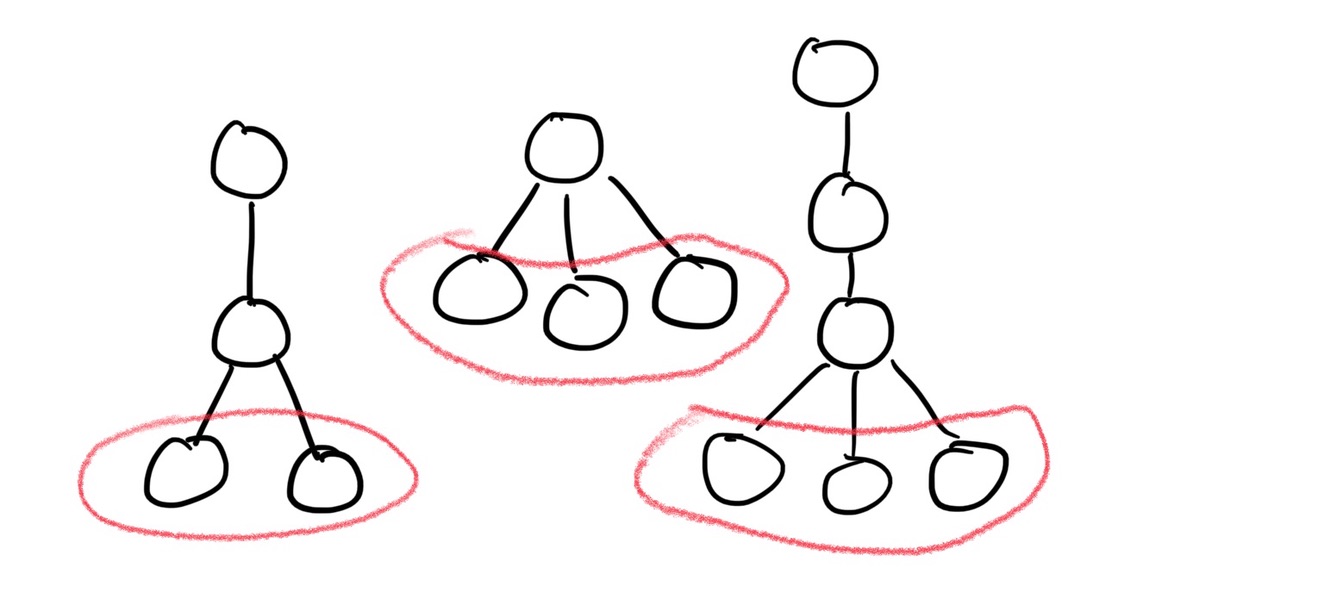
그런데, 한 팀의 팀장을 전체 트리의 루트로 잡아버리면 다른 팀이 만들어질 수 없다.
또한, 루트의 $k$대 독자 후손 노드도 잡아버리면 다른 팀이 만들어질 수 없다.
따라서 1번 노드에서부터 DFS를 돌리다가 처음으로 자식 노드가 2개 이상이 된다면 가장 큰 2개만 골라주면 된다.
필자의 코드이다.
Subtask: $N\le 5\ 000,\ P_i=i-1$ (12점)
직선형 그래프에서 문제를 풀면 된다.
Kadane 알고리즘과 꽤 비슷하다.
각 노드 $i$마다 $\sum_{i\le k\le j}V_k$가 최대가 되게 하는 가장 작은 후손 노드 $j$를 찾을 수 있는데 이는,
노드 $i$를 팀장으로 하는 팀은 $[i,j]$가 된다는 의미이다.
그렇게 찾은 뒤, 모든 정점 쌍 $(a,b)$에 대해서 노드 $a$의 구간, 노드 $b$의 구간이 겹치지 않는다면 그 합을 최대로 갱신시켜가면 풀 수 있다.
Subtask: $P_i=i-1$ (20점)
Subtask #2의 $O(n^2)$ 풀이를 $O(n)$으로 최적화시키면 된다.
노드 $i<j$라면 최대 팀 구간의 끝 부분도 $i$보다 $j$가 크다.
따라서 두 포인터로 최적화 할 수 있다.
그리고 나서 정점 쌍을 확인하는 것은 누적 최대 배열을 이용하면 된다. 반대쪽부터 누적되는 최대 배열을 만들어서 정점 $i$의 최대 팀 구간의 끝 부분$+1$ 위치의 값을 더해주어 갱신시키는 작업을 반복하면 된다.
Subtask #2-3에 대한 필자의 코드다.
Subtask: $N\le 400$ (16점)
$\text{dp}(i):=$노드 $i$의 최대 팀 실력.
$\text{use}(i):=$노드 $i$의 최대 팀의 팀원들.
그렇다면 $\text{dp}(i)=\sum_{j\in C_i} \max\{0,\text{dp}(j)\}$가 된다. 물론 $C_i$는 $i$의 자식 노드 집합이다.
이 때, $\text{dp}(j)>0$인 $j$들이 팀에 포함되므로 재귀적으로 $\text{use}(i)\leftarrow \text{use}(i)+\text{use}(j)$를 반복해주면 된다.
Subtask: $N\le 5\ 000$ (17점)
Subtask #4가 생각해보니까 $O(n^2)$이라서 Subtask #5까지도 한번에 먹힌다.
게다가 Subtask #2는 덤이다.
Subtask #1, #3-4에 대한 필자의 코드다.
Fulltask: $N\le 2\cdot 10^5$ (18점)
Subtask #5의 난이도에 비해 Fulltask의 난이도가 확 높아지는데에 비해서...
18점밖에 주지 않는다...
$\displaystyle \text{best1}(i):=\max_{j\in T_i} \text{dp}(j)$.
$\displaystyle \text{best2}(i):=\max_{j\in T_i,\ j\not \in \text{use}(i)} \text{dp}(j)$.
물론 $T_i$는 노드 $i$를 루트로 하는 서브트리이다.
노드 $i$에 대해 후손 노드와는 $\text{dp}(i)+\text{best2}(i)$를 정답에 갱신해주고,
그렇지 않은 경우는 Subtask #1때의 느낌으로 $\max_{i,j\in C_k} \max \{\text{best1}(i)+\text{best1}(j)\}$을 정답에 갱신해주면 된다.
저런 정의를 세워서 문제에 사용하는 아이디어가 어렵지, 점화식은 간단하다.
$\displaystyle \text{best1}(i):=\max \{ \text{dp}(i),\ \max_{j\in C_i} \text{best1}(j)\}$.
$\displaystyle \text{best2}(i):=\max_{j \in C_i} \{ \text{best1}(j) \text{ if } \text{dp}(j) \le 0 \text{ else } \text{best2}(j)\}$.
#include <bits/stdc++.h>
using namespace std; using ll = long long;
#define rep(i,a,b) for (auto i = (a); i <= (b); ++i)
#define size(x) int((x).size())
#define Mup(x,y) x = max(x,y)
const int N = 2e5+3;
int n, P[N];
ll V[N], answer = -1e18;
vector<int> C[N];
ll dp[N], best1[N], best2[N];
void dfs(int s = 1) {
dp[s] = V[s];
best1[s] = best2[s] = -1e18;
priority_queue<ll> pq;
for (int u : C[s]) {
dfs(u);
Mup(best1[s], best1[u]);
pq.push(best1[u]);
if (dp[u] > 0) {
dp[s] += dp[u];
Mup(best2[s], best2[u]);
} else {
Mup(best2[s], best1[u]);
}
}
Mup(best1[s], dp[s]);
Mup(answer, dp[s]+best2[s]);
if (size(pq) > 1) {
ll v = pq.top(); pq.pop(); v += pq.top();
Mup(answer, v);
}
}
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n;
rep(i,1,n) {
cin >> V[i] >> P[i];
if (i != 1) C[P[i]].push_back(i);
}
dfs();
cout << answer;
}
'PS 문제들' 카테고리의 다른 글
| [KOI 2018 본선] 조화로운 행렬 ★ (0) | 2022.05.21 |
|---|---|
| [JOISC 2019 Day 1] Examination(시험) ★ (0) | 2022.05.17 |
| USACO 2022 US Open Silver Contest ★ (0) | 2022.03.30 |
| USACO 2021 January Contest - Silver (0) | 2022.02.01 |
| USACO 2019 January Contest - Silver ★ (0) | 2021.08.06 |