문제에 풀 때 사용할 수 있는 자료구조 테크닉(문제 특성에 비해 약간 오버킬)을 배울 수 있어 좋았다.
또한, 풀이만 6개를 확인했는데... 진짜 이런 고난이도에 조건이 적은 문제는 여러 방법으로 접근할 수 있구나... 싶었다.
1. Subtask: N≤3 000,Q≤3 000 (2점)
2. Subtask: 점수 ≤105,Zj=0 (20점)
난이도가 확 뛴다.
우선, 각 점수 쌍들을 좌표로서 해석하면 시각화가 되므로 풀이에 접근하기 좋다.
시각화 이후에 간단한 관찰들을 바탕으로 떠오르는 자료구조들이 있을 것이다.
그렇게 다음의 3가지 풀이가 있다:
Merge sort tree | Sweeping | Divide and conquer
사실상 Divide and conquer 방법이라면, 풀태에 다 도달한 것이나 마찬가지라 적지 않겠다.
3. Subtask: 점수 ≤105,Zj≤2⋅105 (21점)
Fulltask 풀이에다가 좌표압축 안 했을 때 얻는 서브태스크인데, 스위핑하면서 좌표압축 모르는 사람도 있을지 의문이다 ㅋㅋ
따라서 풀이는 Fulltask에 적도록 하겠다.
4. Fulltask: N,Q≤105, 점수 ≤109,Zj≤2⋅109 (57점)
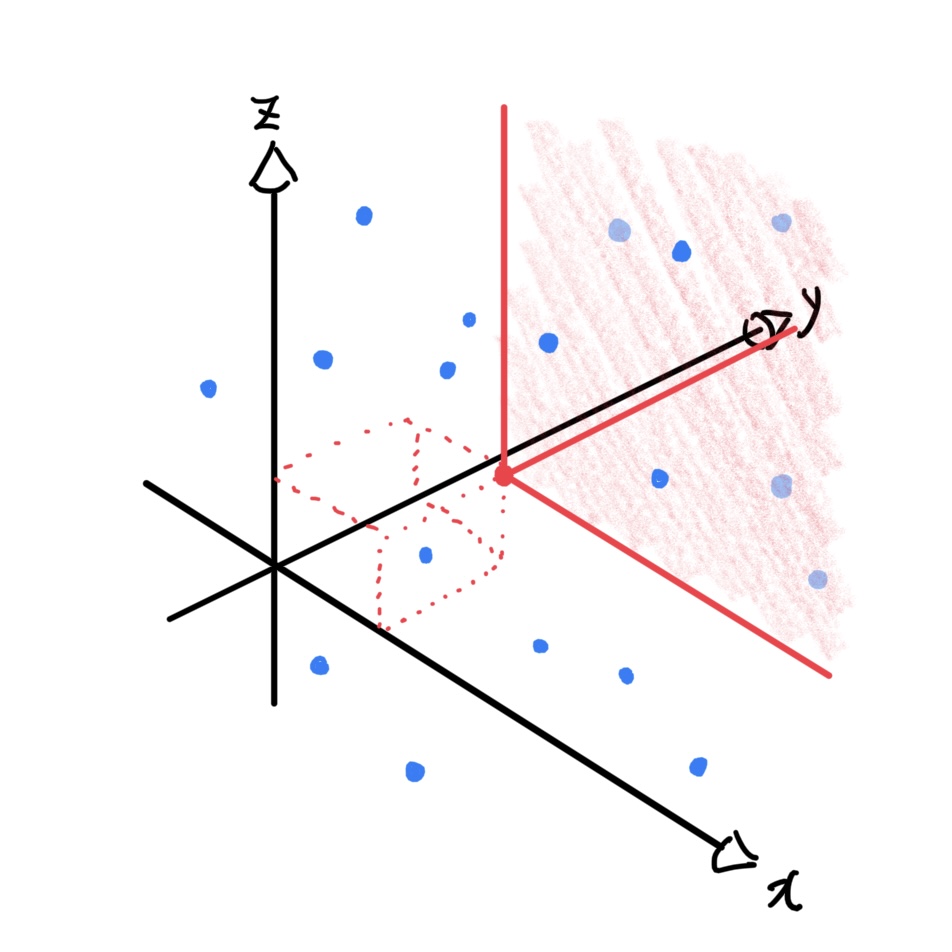
각 학생 i의 정보는 (Si,Ti)로 표현된다. 각 교수 j의 커트라인은 (Xj,Yj,Zj)로 표현된다.
문제의 조건을 생각하면 이는 다시, 각 (Si,Ti,Si+Ti)를 공간 상에 찍은 뒤
교수 j마다 커트라인 축 Xi,Yi,Zi를 넘기는 방향의 8분할된 공간에 포함되는 점의 개수를 구하는 문제로 생각할 수 있다.

그러면 이 문제는 3차원 쿼리 문제이다.
그런데, Subtask #2의 Sweeping 아이디어를 이용한다면 1차원을 낮출 수 있다.
단순하게는 2D Segment tree을 이용해 평면을 스위핑 해주면 되는데, 구현이 힘들고 메모리가 큰 관계로 더 간단한 풀이가 좋을 것 같다. 무엇보다 내가 2D 세그를 안 짜봤다.
4.1. Solution 1
"CDQ 알고리즘"과 스위핑을 이용해 푼다.
2차원 스위핑 문제를 분할 정복을 이용해서 업데이트를 없애준 뒤 1차원 스위핑 문제로 바꿔줄 수 있다.
분할 정복 과정에서 가운데를 기준으로 한쪽은 업데이트, 반대쪽은 쿼리로 쌍을 지으면서 올라오면 된다.
스위핑 이동 방향이 −x축 방향이라고 잡게 되면 x,z에 대한 조건은 성립하기 때문에 y값들을 관리하는 펜윅 트리를 들고 스위핑해주면 된다.
정리하면,
3차원 업데이트 없는 문제
⇒ 평면 스위핑 문제
⇒ 분할 정복을 이용한 2차원 업데이트 없는 문제
⇒ 분할 정복과 스위핑을 이용한 직선 스위핑 문제로 바뀐다.
참고로 시간 복잡도는 O((n+q)log2(n+q))가 된다.
<c++ />
#include <bits/stdc++.h>
using namespace std; using ll = long long;
#define rep(i,a,b) for (auto i = (a); i <= (b); ++i)
#define all(x) (x).begin(), (x).end()
const int N = 1e5+3, Q = 1e5+3;
int n, q;
ll answer[Q], t[N+Q+1];
struct point { int x, y, z, i; } p[N+Q];
void add(int k, ll x){ for (++k; k <= N+Q; k += k&-k) t[k] += x; }
ll sum(int l, int r){ ll s = 0;
for (++r; r >= 1; r -= r&-r) s += t[r];
for (; l >= 1; l -= l&-l) s -= t[l];
return s;
}
void dnc(int a = 1, int b = n+q){
if (a == b) return;
int m = (a+b)/2;
dnc(a,m), dnc(m+1,b);
vector<point> v;
rep(i,a,m) if (!p[i].i) v.push_back(p[i]);
rep(i,m+1,b) if (p[i].i) v.push_back(p[i]);
sort(all(v),[](auto &a, auto &b) {
return make_tuple(a.x,a.y,-a.i) > make_tuple(b.x,b.y,-b.i);
});
for (auto &[x,y,z,i] : v) {
if (i) answer[i] += sum(y,n+q);
else add(y,+1);
}
for (auto &[x,y,z,i]: v) if (!i) add(y,-1);
}
int main(){
cin.tie(0)->sync_with_stdio(0);
cin >> n >> q;
vector<int> ys;
rep(i,1,n) {
cin >> p[i].x >> p[i].y;
ys.push_back(p[i].y);
p[i].z = p[i].x+p[i].y;
p[i].i = 0;
}
rep(j,n+1,n+q) {
cin >> p[j].x >> p[j].y >> p[j].z;
ys.push_back(p[j].y);
p[j].i = j-n;
}
sort(all(ys)), ys.erase(unique(all(ys)),end(ys));
rep(k,1,n+q) p[k].y = lower_bound(all(ys),p[k].y)-begin(ys);
sort(p+1,p+n+q+1,[](auto &e1, auto &e2) {
if (e1.z != e2.z) return e1.z > e2.z;
return e1.i < e2.i;
});
dnc();
rep(j,1,q) cout << answer[j] << '\n';
}
4.2. Solution 2
관찰을 이용하면 특별한 테크닉 없이 스위핑 만으로도 해결할 수 있다. 물론 이 문제에 국한된 풀이이다.
Xj+Yj<Zj인 경우와 Xj+Yj≥Zj인 경우로 나누면 되는데, 후자는 사실상 Zj를 무시해도 되므로 Subtask #2의 아이디어를 이용하면 된다.
전자가 새로운 경우인데, 이 때 Si+Ti의 감소 방향으로 스위핑을 진행하면서, 포함배제를 이용하면 된다.
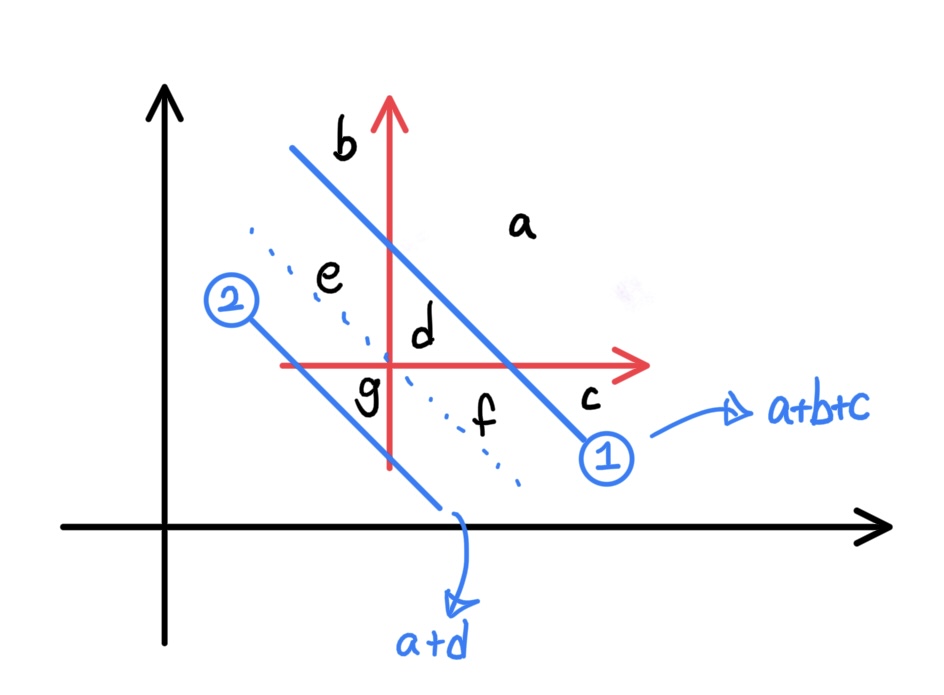
아래 그림의 ①이 지금 논의중인 상태이다. d=∅,e=∅,f=∅이다.
|a|=|a+d|=|a+b+e+d|+|a+d+c+f|−|a+d|인데, 단순 x축, y축 스위핑으로 계산할 수 있다.
<c++ />
#include <bits/stdc++.h>
using namespace std; using ll = long long;
#define rep(i,a,b) for (auto i = (a); i <= (b); ++i)
#define all(x) (x).begin(), (x).end()
const int N = 1e5+3, Q = 1e5+3;
int n, q;
ll answer[Q];
struct point { int x, y, z, i; } p[N];
template <const int N> struct fenwick_tree {
ll t[N+1] {0,};
void add(int k, ll x){ for (++k; k <= N; k += k&-k) t[k] += x; }
ll sum(int l, int r){ ll s = 0;
for (++r; r >= 1; r -= r&-r) s += t[r];
for (; l >= 1; l -= l&-l) s -= t[l];
return s;
}
};
void solve1(vector<point> &query){ // X+Y < Z
fenwick_tree<N+Q> sweepX, sweepY;
sort(p+1,p+n+1,[](auto &a, auto &b){ return a.z > b.z; });
sort(all(query),[](auto &a, auto &b){ return a.z > b.z; });
int j = 1;
for (auto [x,y,z,i] : query) {
while (j <= n and z <= p[j].z) {
sweepX.add(p[j].x,+1);
sweepY.add(p[j].y,+1);
++j;
}
answer[i] = sweepX.sum(x,n+q)+sweepY.sum(y,n+q)-j+1;
}
}
void solve2(vector<point> &query){ // X+Y >= Z
fenwick_tree<N+Q> sweep;
sort(p+1,p+n+1,[](auto &a, auto &b){ return a.x > b.x; });
sort(all(query),[](auto &a, auto &b){ return a.x > b.x; });
int j = 1;
for (auto [x,y,z,i] : query) {
while (j <= n and x <= p[j].x) sweep.add(p[j++].y,+1);
answer[i] = sweep.sum(y,n+q);
}
}
int main(){
cin.tie(0)->sync_with_stdio(0);
cin >> n >> q;
vector<point> q1, q2;
vector<int> xs, ys;
rep(i,1,n) {
int s, t; cin >> s >> t;
p[i] = {s,t,s+t,0};
xs.push_back(s);
ys.push_back(t);
}
rep(i,1,q) {
int x, y, z; cin >> x >> y >> z;
if (x+y < z) q1.push_back({x,y,z,i});
else q2.push_back({x,y,z,i});
xs.push_back(x);
ys.push_back(y);
}
sort(all(xs)), xs.erase(unique(all(xs)),end(xs));
sort(all(ys)), ys.erase(unique(all(ys)),end(ys));
rep(i,1,n) p[i].x = lower_bound(all(xs),p[i].x)-begin(xs);
rep(i,1,n) p[i].y = lower_bound(all(ys),p[i].y)-begin(ys);
for (auto &q : q1) q.x = lower_bound(all(xs),q.x)-begin(xs);
for (auto &q : q2) q.x = lower_bound(all(xs),q.x)-begin(xs);
for (auto &q : q1) q.y = lower_bound(all(ys),q.y)-begin(ys);
for (auto &q : q2) q.y = lower_bound(all(ys),q.y)-begin(ys);
solve1(q1), solve2(q2);
rep(i,1,q) cout << answer[i] << '\n';
}
4.3. Solution 3
Indexed set + 펜윅으로 2D 세그 스위핑와 거의 동일한 느낌으로 풀 수 있다.
아마 구현이 제일 쉬울거다! 대신 상수가 커서 시간이 오래 걸리니 주의...
<c++ />
#include <bits/stdc++.h>
using namespace std; using ii = pair<int,int>; using ll = long long;
#define rep(i,a,b) for (auto i = (a); i <= (b); ++i)
#define all(x) (x).begin(), (x).end()
#include <ext/pb_ds/assoc_container.hpp>
using namespace __gnu_pbds;
template <class T> using indexed_set
= tree<T,null_type,less<>,rb_tree_tag,tree_order_statistics_node_update>;
const int N = 1e5+3, Q = 1e5+3;
int n, q;
ll answer[Q];
struct point { int x, y, z, i; } P[N+Q];
indexed_set<ii> t[N+Q+1];
void add(int k, int v) {
static int f = 0;
for (++k, ++f; k <= N+Q; k += k&-k) t[k].insert({v,f});
}
ll sum(int l, int r, int v) {
ll s = 0;
for (++r; r >= 1; r -= r&-r) s += size(t[r])-t[r].order_of_key({v,0});
for (; l >= 1; l -= l&-l) s -= size(t[l])-t[l].order_of_key({v,0});
return s;
}
vector<int> ys;
int c(int x) { return lower_bound(all(ys),x)-begin(ys); }
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n >> q;
rep(i,1,n) {
cin >> P[i].x >> P[i].y;
ys.push_back(P[i].y);
P[i].z = P[i].x+P[i].y, P[i].i = 0;
}
rep(i,n+1,n+q) {
cin >> P[i].x >> P[i].y >> P[i].z;
ys.push_back(P[i].y), P[i].i = i-n;
}
sort(all(ys)), ys.erase(unique(all(ys)),end(ys));
sort(P+1,P+n+q+1,[](auto &a, auto &b){
return make_tuple(a.x,a.y,a.z,-a.i) > make_tuple(b.x,b.y,b.z,-b.i);
});
rep(i,1,n+q) {
if (P[i].i) answer[P[i].i] = sum(c(P[i].y),n+q,P[i].z);
else add(c(P[i].y),P[i].z);
}
rep(i,1,q) cout << answer[i] << '\n';
}
4.4. Other Solutions
5. 디버깅
Merge sort tree 풀이를 짜고서, 좌표의 중복이 가능하여 리프 노드들에 대한 정렬도 진행해야 하는데, 이를 빠뜨렸다!!!
이걸로 미친듯이 오래 걸리는 디버깅을 진행했다.
앞으로 절대 이걸로 실수하지 말아야지!!
dnc() 호출 이전에 정렬했던 것의 정렬 기준이 return e1.i > e2.i;로 되어 있었다...
'실수 노트'에 "2번째 비교 조건을 꼼꼼히 따져보기"를 넣어야겠다.
6. 참고
'PS 문제들' 카테고리의 다른 글
| [IOI 2005 Day 1] Garden(정원) ★ (0) | 2022.05.22 |
|---|---|
| [KOI 2018 본선] 조화로운 행렬 ★ (0) | 2022.05.21 |
| [KOI 2021 1차 중등부] 두 개의 팀 ★ (0) | 2022.05.16 |
| USACO 2022 US Open Silver Contest ★ (0) | 2022.03.30 |
| USACO 2021 January Contest - Silver (0) | 2022.02.01 |