저는 2020년도 말에 알고리즘 분야(PS)를 접하게 되었습니다. 2023년에 들어서 운 좋게 SUAPCw의 Call for Tasks에 뽑히게 된 것을 시작으로 6개의 대회에 운영진으로 참가하였습니다. 또한 3개의 개인 문제를 검수하였습니다. 이 글을 쓰는 시점에서 5개의 개인 문제 검수와 1개의 대회 출제/검수를 진행 중에 있습니다.dohoon의 만든 문제dohoon의 검수한 문제네이버 블로그에 후기를 남겨 왔지만 개인적인 내용이 담겨 있어서 대부분 공개를 하지는 않았습니다. 대신 이렇게 티스토리 블로그를 통해 전반적으로 정리하여 다른 분들께 도움이 되는 대회 운영/출제/검수에 관한 시행착오들을 기록해보고자 합니다. 짧은 후기 모음Codeforces Round #851 (Div.2)테스터로 참여했습니..

KOI는 Korean Olympiad in Informatics의 약자로, 한국 정보 올림피아드를 말합니다. 이 대회는 1차 대회와 2차 대회로 이루어져 있고, 1차 대회는 이산 수학을 바탕으로 하는 수학 문제들로 이루어진 1교시와 알고리즘 문제들로 이루어진 2교시로 나누어 진행됩니다. 자세한 정보는 koi.or.kr에서 확인하실 수 있습니다. koi.or.kr에 2교시 문제들의 풀이는 공개되어 있지만 1교시 문제들의 풀이는 제공하지 않아서 풀이를 작성했습니다. 팀원 찾기: 엄밀한 증명 고민 중... 1교시 풀이 문제의 지문은 링크에서 확인하실 수 있습니다. 또한, biko.kr에서 문제를 채점받을 수 있습니다. 다음은 각 문제에 대해 개인적으로 부여한 난이도와 실제 배점입니다. 1. 그래프의 지름 2...

이 글에서는 구간 트리(segment tree), 펜윅 트리(fenwick tree), 느리게 갱신되는 구간 트리(segment tree with lazy propagation)들이 성립하는 조건을 알아볼 것이다. 다만, 이 글에는 한계가 존재한다. 구간 트리를 하나의 Black-Box(기능은 알지만 작동 원리를 이해할 수 없는 복잡한 기계 장치나 시스템, 물체)로 바라보기 때문에 직사각형들의 합집합의 넓이를 구하는 문제와 같이 구간 트리의 구조를 변형시키는 문제에는 이 글의 내용이 적용이 되지 않을 수 있다. 기본 질의응답의 대상인 배열은 $[a_1,a_2,\ldots,a_n]$이다. 배열 속 원소들을 포함하는 집합 $S$, 원소들 간의 이항 연산 $*$, 갱신 함수의 집합 $F$가 있다. 이때, 당연..

개인적으로 백준에서 보는 것보다 pdf로 보는 게 더 편한 것 같다. 선발고사 문제 치고는 꽤 쉽다. 하지만 구현이 만만치 않다... 예제 속 그림을 보면 중요한 관찰이 눈에 쉽게 보인다. 바로 두 경로는 수직 구간 혹은 수평 구간을 정확히 하나 공유한다는 것이다. 이를 바탕으로 수평에 대해서 한 번 풀어주고, 수직에 대해서 같은 방식으로 한 번 풀어준다고 생각하고 한쪽만 고려해보자. 수직 구간을 공유한다면 수직 구간의 양 끝점을 기준으로 경로가 정확히 나뉜다. 이를 구간합 배열을 잘 이용하여 합쳐주면 된다. 솔직히 좋은 문제는 아니라고 생각한다... #include #define rep(i,a,b) for (auto i = (a); i = (a); --i) #define siz(x) int((x).si..

개인적으로 백준에서 보는 것보다 pdf로 보는 게 더 편한 것 같다. 한 자릿수 서브태스크 배점들을 보고 왜 이렇게 짜게 주나 했는데, 하나씩 풀다 보니까 기가 막힌 점수 배분인 것 같다. 부분 문제 1 ~ 4 풀이는 노드의 번호를 1-base 기준으로 작성했고, 부분 문제 5 풀이는 0-base 기준으로 작성했습니다. 궁금하신 점은 댓글로 남겨주시면 답변해 드리겠습니다! 문제 요약 "모든 $[i,j]$꼴의 정점 집합에 대해 만들어진 각 virtual tree의 가중치의 합을 구하라." 정도이다. 부분 문제 1 (5점) $N\le 300$이다. $O(N^3)$이 넉넉하게 돌아갈 수준이다. 모든 $[i,j]$를 직접 돌면서 dfs를 돌리면 된다. 웬만해서는 코드를 짜보려고 했는데, 점수 대비 구현량의 가성..

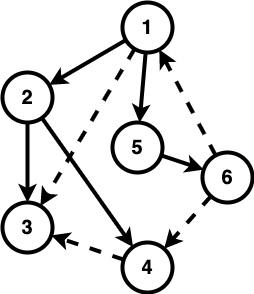
이 블로그의 "그래프에 관하여" 시리즈의 첫 번째 카테고리, ❮DFS 트리❯의 개요이다. DFS 트리는 DFS를 응용한 다양한 알고리즘들을 이해하기 위한 좋은 표현법이자 도구이다. 조금 어려운 감이 있지만 꼼꼼히 이해한다면 큰 도움이 될 것이라고 생각한다. DFS 트리/포레스트란? 어떤 연결 그래프에서 DFS 순회하는 과정을 그렸을 때 나타나는 유향 신장 트리(directed spanning tree)를 DFS 트리라고 한다. 당연히 여러 개가 존재할 수 있다. 연결 그래프가 아닐 경우에는 각 연결 컴포넌트마다 DFS 트리를 만들 수 있으니 DFS 포레스트로 확장해서 생각할 수 있다. 유향 그래프일 경우, DFS 트리의 간선들을 네 가지로 분류할 수 있다. 트리 간선(tree edge): DFS 트리에 ..

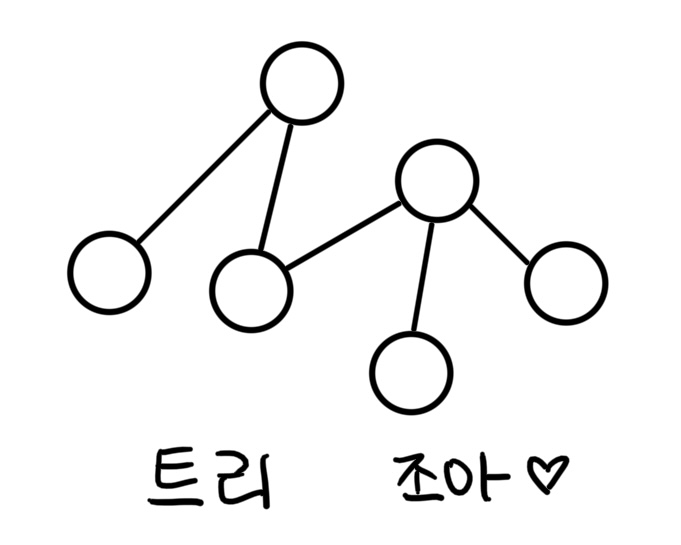
이 블로그의 "트리에 관하여" 시리즈의 첫 번째 카테고리, ❮Tree DP❯에서 다루는 첫 번째 주제이다. 이 테크닉은 다른 이름으로도 알려져 있다. KOI에 출제된 어떤 유명한 문제의 이름을 딴 것인데, 스포일러가 될 수 있으므로 연습 문제 목차에서 후술 하겠다. Square-order tree DP?사실 이건 그 자체로 뭔가 해야 하는 테크닉은 아니다. 트리 DP 점화식이 2차원으로 나오고, 전이 과정을 합쳐서 대충 보기에는 $O(n^3)$의 시간 복잡도를 가져야 할 것으로 보이는 후술 할 조건을 만족하는 알고리즘이 사실 $O(n^2)$이라는 더 좋은 시간 복잡도를 갖는다는 사실을 이용하는 테크닉이다. 만족해야 하는 조건은 구한 점화식 $\text{dp}(x,y)$에 대해, $x$가 각 노드를 뜻하고..

https://youtu.be/S2N8VTdL0og 환경 운영체제: Mac OS 사용 에디터: Visual Studio Code 터미널: zshrc 동기 tasks.json을 편집하는 것이 개인적으로 어렵다고 느껴짐... 간단한 터미널 명령어들을 이용해 손쉽게 컴파일/실행/테스트 해보자! 사용한 터미널 명령어 compile(){ g++-12 -Wall -O2 -std=c++17 -o base cpp/base.cpp cpp/grader.cpp } g++-12: 컴파일러 종류 -Wall: 컴파일 경고 옵션 -O2: 최적화 옵션 -std=c++17: 사용 언어 -o base: 실행 파일을 base라는 이름으로 설정 cpp/base.cpp cpp/grader.cpp: 컴파일에 사용되는 파일들 run(){ com..