매일의 문제 풀이를 기록합니다. 여기서 문제 풀이란, 알고리즘 문제 해결을 의미합니다. 백준/코드포스/앳코더 등의 플랫폼을 이용합니다.
완성도가 높은 글이 아닙니다. 대신 생각의 흐름이 꽤 자세하게 적혀 있을 것 같네요.
핀볼
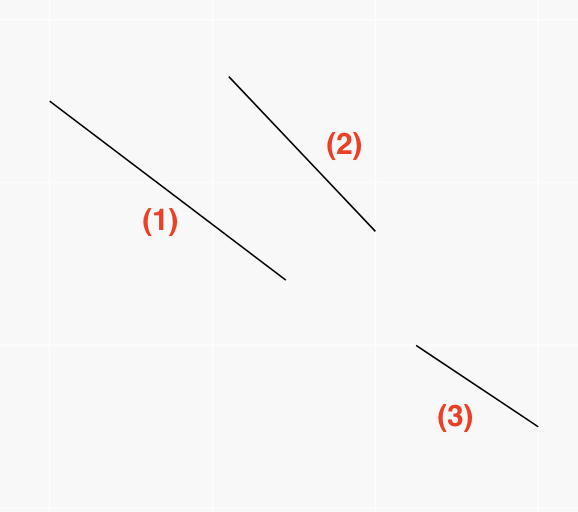
- 결국 어떤 선분이 더 위에 있는지를 쉽게 안다면 그것부터 차례대로 봐주면 됩니다.
- 겉보기에는 매우 단순해 보여서 막 정렬 조건을 짜게 됩니다.
- 그러면 예제에서 무한 루프가 돕니다.
- Strict Weak Ordering을 만족하지 않기 때문입니다.
- SWO에는 한 4가지 조건이 있는데 그중 '비비교성의 추이성'에서 문제가 생깁니다.
- 따져보면, 비교 가능한 관계를 $\sim$이라고 할 때,
- $(3)\not \sim (1)$이고 $(3)\not \sim (2)$인데, $(1)\sim (2)$이기 때문에 문제가 생깁니다.
- 암튼.. 목표는 순서 관계에 대한 transitive reduction?을 구하는 것인데요.
- 스위핑으로 해결이 가능하다는 것 같습니다.
- 발상이 신기하네요.
- 맞히고 돌아오겠습니다.
USACO 23/24 Dec
- 콘테스트가 전부 종료된 이후 글을 수정했습니다.
- A번
- $N\le 750$ 제한이 굉장히 눈에 띕니다.
- $O(n^3)$이 될 테니 Floyd-Warshall이나 구간 DP를 고려할 수 있습니다.
- 짧은 구간부터 보면서 이을지 말지를 결정하면 됩니다.
- 카운팅 중에 중복이 발생하지 않도록 $u\le k\le v$인 $k$를 볼 때, $u\to k$인 direct 직선이 있는지 확인해서 세어줍니다.
- bool의 overflow로 쉽게 구현할 수 있을 것이라 생각했지만, UB인지 잘 안 되어서 고쳤더니 맞았습니다.
- B번
- DAG가 주어집니다.
- 우선 최장경로의 길이만 구하는 것이 목적이라면 아마 백준의 "ACM Craft" 문제와 아주 비슷하게, 어쨌건 위상정렬이건 하향식 DP건 해서 할 수 있다는 걸 알 수 있습니다.
- 사전순으로 최소를 만족시키는 것이 문제입니다.
- 최장경로의 길이가 고정되어 있다는 점 덕분에 문제가 수월해집니다.
- 문자열을 각 정점마다 직접 들고 있을 수는 없을 텝니다.
- 따라서 해시 값이나 부분 문자열의 위치 등을 관리하는 방법이 있을텐데, 한 문자열 위에서 벌어지는 문제가 아니기 때문에 부분 문자열의 위치를 고려하는 방향은 어려울 듯 합니다.
- 최장경로의 길이가 고정되었다는 점에 착안하여, 최장경로로 이어진 어느 정점에서부터의 최장경로를 전체에서도 그대로 suffix로 갖는다는 성질을 알 수 있습니다.
- 그럼 뒤에 나오는 것부터 차례대로 처리하여 현재 정점에서 잘 선택만 해주면 되겠습니다.
- 우선 이를 위해 번거로운 간선들을 미리 삭제해 둘 수 있습니다. 최장경로에 미치지 못하는 방향의 간선, 최장경로이지만 가중치가 최솟값이 아닌 간선들을 제거하면 됩니다.
- 여러 고민을 하다 보면 $2^k$ 단위로 해시값을 따와서 LCP를 확인할 수 있다는 착안을 할 수 있습니다. suffix array를 알고 있다면 떠올리기 조금 더 수월할 것 같습니다.
- 저는 문자열 연습이 부족해서 이러한 발상이 조금 늦었습니다. 한 40분 이상 걸리지 않았나 싶네요.
- 아무튼 이걸 그대로 해주면 되는데 구현이 굉장히 복잡합니다.
- 미리 계획을 잘 세워두고 구현에 임하자는 각오를 여러번 다졌습니다.
- 전체적으로 코딩을 한 번 끝내기까지 대충 40분~1시간 정도가 걸리지 않았나 싶습니다. 다음에는 시간을 잘 재보고 싶네요.
- 그러고서 기나긴 디버깅에 40분~1시간 정도를 박은 것 같습니다.
- 오류의 원인은 재귀 함수에서 자신을 호출하지 않은 것이 문제였습니다.
- 그런데 예제가 다 맞아서... 다른데 삽질하다가 시간을 많이 날렸네요.
- C번
- 너무 풀이가 보이길래 파라매트릭을 돌리거나 각 x를 다 확인해주는 방법 같은 걸로 해보려고 했습니다.
- 파라매트릭은 RE가 나길래 살짝 바꿔서 x를 다 확인해주는 코드를 제출하려다가 끝났버렸습니다...
- 아쉽네요. 이번 컨테스트는 난이도가 많이 쉬워서 좋은 찬스였는데 놓쳐버렸습니다. 하지만 다음에는 올릴 수 있겠죠?!
