배열과 gcd
난이도가 P3보다 높아져야 하는 문제라고 생각한다.
풀이
$\mathrm{let\ }b_i=C_{i-1},\ G_i=C_i,\ b_i=B_i\times G_i.$
$\mathrm{let\ }x_i=X_i\times G_i.$
만약 $G_i\nmid b_i$였다면 $0$을 출력하고 프로그램을 종료한다.
그러면 문제는 각 $i(\ge 2)$에 대해 $\left [1,\lfloor \frac {num} {G_i}\rfloor \right ]$ 속의 $B_i$와 서로소인 $X_i$의 개수를 구해서 전부 곱하는 문제로 바뀐다. (가능한 모든 $X_i$에 대해 $x_i$는 $a_i$로 가능한 모든 값들이다.)
euler totient 함수를 변형해보겠다는 생각도 해볼 수 있지만 힘들다.
어쩌면 소인수들에 대한 포함 배제를 이용하여 서로소의 개수를 구할 수 있을 것이다.
애초에 euler totient 함수의 공식을 유도하는 방법 중 하나도 포함 배제이다.
포함 배제를 이용했을 때, $f(n):=(n$의 소인수의 개수$)$라 하면, 시간 복잡도는 $O(2^{|f(B_i)|})$이 된다.
$f(n)=O(\log n)$이다.
$B_2\times B_3\times \cdots \times B_n=\frac {C_1} {C_n}$임을 알고 있다. 지수-로그 법칙을 이용해 식을 변형하자.
$\log B_2 + \log B_3 + \cdots + \log B_n = \log \left (B_2\times B_3\times \cdots \times B_n\right )=\log \left (\frac {C_1} {C_n} \right )$이므로, 전체 시간 복잡도는 $O(n+2^{\log C_1} )=O(n+C_1)$가 된다는 것을 알 수 있다.
#include <bits/stdc++.h>
using namespace std; using ii = pair<int,int>; using ll = long long;
#define rep(i,a,b) for (auto i = (a); i <= (b); ++i)
#define per(i,a,b) for (auto i = (b); i >= (a); --i)
#define all(x) begin(x), end(x)
#define siz(x) int((x).size())
#define Mup(x,y) x = max(x,y)
#define mup(x,y) x = min(x,y)
#define fi first
#define se second
#define dbg(...) fprintf(stderr,__VA_ARGS__)
#pragma region modnum template from ecnerwala/cp-book
// https://github.com/ecnerwala/cp-book/blob/master/src/modnum.hpp
...
#pragma endregion modnum template
using mint = modnum<1'000'000'007>;
const int N = 1e5+3;
int n, k, c[N];
vector<int> factors(int m) { // 1'000
vector<int> res;
for (int x = 2; x*x <= m; ++x) {
if (m%x == 0) {
res.push_back(x);
while (m%x == 0) m /= x;
}
}
if (m > 1) res.push_back(m);
return res;
}
// 2*3*5*7*11*13*17*19*23*29 > 6e9
// |p| <= 10
mint solve(int x, int y) { // 10'240
auto p = factors(y);
mint res = 0;
rep(b,0,(1<<siz(p))-1) {
int z = x;
rep(i,0,siz(p)-1) if (b>>i&1) z /= p[i];
if (__builtin_popcount(b)%2) res -= z;
else res += z;
}
return res;
}
int main() {
scanf("%d %d", &n, &k);
rep(i,1,n) scanf("%d", &c[i]);
// dbg("[1,%d]에서 %d와 서로소인 수의 개수 = %d\n", 1, 1, int(solve(1,1)));
mint ans = 1;
rep(i,2,n) {
int b = c[i-1], G = c[i];
if (b%G) puts("0"), exit(0);
int B = b/G;
ans *= solve(k/G,B);
}
printf("%d", int(ans));
}
램프
얘는 반대로 P3까지 낮아져야 한다고 본다.
풀이
cyclic한 상태니까 0-base가 편하다.
초기의 배열을 $a_0,a_1,\ldots,a_{n-1}$이라고 하자.
한 번의 연산을 적용한 배열을 $a'$이라고 하자.
$a'_i=\begin{cases} a_i&\text{if}\;a_{i+1\text{ mod }n}=0\\ \sim a_i&\text{if}\;a_{i+1\text{ mod }n}=1 \end{cases}$
이를 다시 생각하면, $a'_i=a_i\oplus a_{i+1}$라는 것을 알 수 있다.
문제의 조건에 따라 큰 $m$번의 연산을 적용한 결과를 빠르게 구하기 위해서는 어떤 로그 단위의 점프를 해나갈 수 있으면 한다. 따라서 이진수에 초점을 맞춰 관찰하자.
$a_{j,i}=a_{j-1,i}\oplus a_{j-1,i+1}$이라 하고 $a_{0,i}=a_i$라고 한 뒤 작은 경우에 대해 식을 정리해보자.
$a_{2^k,i}=a_{0,i}\oplus a_{0,i+2^k}$임을 관찰할 수 있다. 이 규칙은 더 일반적으로 봤을 때, $j$항이 $2^k$ 차이날 경우에 적용할 수 있을 것이다.
따라서, $m$의 켜진 비트 $k$들에 대해 기존 배열의 값들을 이용하여 $a_{j+2^k,i}=a_{j,i}\oplus a_{j,i+2^k}$를 반복적으로 계산할 수 있다.
#include <bits/stdc++.h>
using namespace std; using ii = pair<int,int>; using ll = long long;
#define rep(i,a,b) for (auto i = (a); i <= (b); ++i)
#define per(i,a,b) for (auto i = (b); i >= (a); --i)
#define all(x) begin(x), end(x)
#define siz(x) int((x).size())
#define Mup(x,y) x = max(x,y)
#define mup(x,y) x = min(x,y)
#define fi first
#define se second
#define dbg(...) fprintf(stderr,__VA_ARGS__)
const int N = 1e6+3;
int n, m, a[N], b[N];
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n >> m;
rep(i,0,n-1) cin >> a[i];
rep(j,0,30) if (m>>j&1) {
rep(i,0,n-1) {
b[i] = a[i] xor a[(i+(1<<j))%n];
}
swap(a,b);
}
rep(i,0,n-1) cout << a[i] << '\n';
}
최고인 대장장이 토르비욘
디버깅하다가 심하게 말렸다.
풀이
각 $i$마다 $s_i,t_i$ 중 하나씩 고른다. 길이로 선택한 요소를 $a_i$, 너비로 선택한 요소를 $b_i$라고 하자.
잘 생각해보면, $i$의 순서는 상관이 없고 그냥 $a_i$가 distinct하면 된다.
이 조건을 만족시키도록 $a_i$를 최대화하면 된다.
우선 문제를 풀기 위한 여러가지 고민을 해보자.
충분히 고민을 해 보았는가?
distinct하게 고른다는 성질을 생각하면 이분 매칭과 비슷하다는 느낌을 받을 수 있다.
그러므로 그래프 모델링을 시도해 볼 수 있다.
이건 필자의 생각이고, 혹시 다른 동기를 갖고 그래프 모델링을 시도했을 경우 댓글에 남겨주면 감사하겠다.
$s_i$와 $t_i$를 잇는 간선을 만들어주자.
이렇게 구성된 양방향 그래프에서 각 간선들에 방향을 부여하자.
$a\to b$ 간선은 $a$를 너비로 사용하고, $b$를 높이로 사용한다는 의미를 내포한다고 하자.
너비가 distinct 해야 하므로, 위 규칙에 의해 각 정점의 out degree는 $1$ 이하가 되어야 한다.
그래프는 여러 개의 연결 컴포넌트로 구성될 것이다. 각각 처리하면 되므로, 하나의 연결 컴포넌트에 대해서만 고려하자.
다음과 같이 그래프가 구성되었을 때, 방향을 부여하는 방법은 한 가지이다.

물론, 사이클의 방향이 반대일 수 있지만 사이클 위의 정점들은 어차피 전부 정확히 한 번씩 사용하므로 결과적으로 같다.

각 정점의 out degree가 $1$ 이하라는 조건은 사실 잘 생각해보면 functional graph에 매우 가깝다는 의미임을 알 수 있다.
out degree가 $0$인 경우가 존재할까? 그렇다. 그럼 최대 몇 개까지 존재할 수 있을까? 한 개이다.
왜냐하면, 각 간선의 방향이 정해질 때 한 정점의 진출 차수를 가져가기 때문에 간선의 개수가 정점의 개수를 넘을 수 없기 때문이다.
정확히는 $|E|\le |V|$인데, 연결 컴포넌트를 가정했으므로 $|V|-1 \le |E|\le |V|$이여서다.
그럼 위의 그래프를 마저 살펴보자. 각 정점은 in degree번 더해진다.
이렇게 더하는 작업은 매우 까다롭다.
따라서 전체 degree에서 out degree를 빼가는 식으로 하자. 왜냐하면 out degree는 전부 $1$로 동일하기 때문이다.
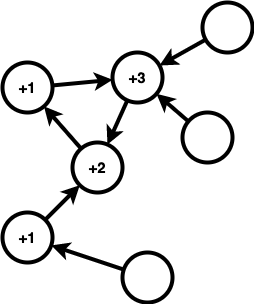
그럼 다음과 같이 다루기 편한 상태가 된다.
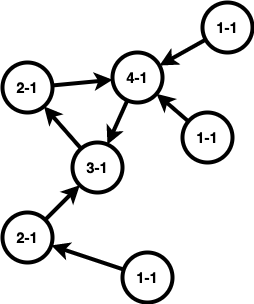
근데, 이 경우는 out degree가 전부 $1$인 경우이다. 하나가 $0$인, 즉 트리 그래프인 경우도 따져보자.
다음과 같이 out degree가 $0$인 정점을 특정하면 이 정점을 바탕으로 루트 트리가 만들어진다. 그리고 이 정점만 더하지 않는다.
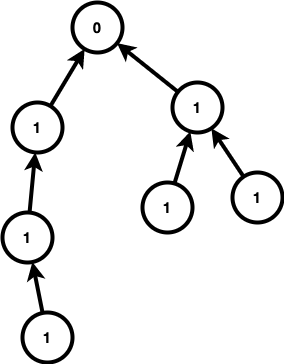
따라서 트리일 경우 제일 값이 작은 노드로 설정해주면 된다.
위의 모든 관찰을 하고 나면 구현은 간단하다. 만약 그래프의 강한 조건들을 관찰하지 못했다면 풀기 매우 어려워졌을 것이다.
#include <bits/stdc++.h>
using namespace std; using ii = pair<int,int>; using ll = long long;
#define rep(i,a,b) for (auto i = (a); i <= (b); ++i)
#define per(i,a,b) for (auto i = (b); i >= (a); --i)
#define all(x) begin(x), end(x)
#define siz(x) int((x).size())
#define Mup(x,y) x = max(x,y)
#define mup(x,y) x = min(x,y)
#define fi first
#define se second
#define dbg(...) fprintf(stderr,__VA_ARGS__)
map<int,vector<int>> adj;
map<int,int> deg;
ii dfs(int s, set<int> &c) {
static map<int,bool> visited;
if (visited[s]) return {0,0};
visited[s] = true;
c.insert(s);
ii res = {1,0}, tmp;
for (auto u : adj[s]) {
res.se++;
if (visited[u]) continue;
tmp = dfs(u,c);
res.fi += tmp.fi;
res.se += tmp.se;
}
return res;
}
int main() {
cin.tie(0)->sync_with_stdio(0);
int n; cin >> n;
set<int> S;
ll ans = 0;
rep(i,1,n) {
int s, t;
cin >> s >> t;
adj[s].push_back(t);
adj[t].push_back(s);
ans += s+t;
S.insert(s), S.insert(t);
}
for (auto s : S) {
set<int> C;
auto [v,e] = dfs(s,C);
assert(e%2 == 0), e /= 2;
if (v == 0 and e == 0) continue;
if (v-1 == e) {
for (auto c : C) ans -= c;
ans += *prev(end(C));
} else {
assert(v == e);
for (auto c : C) ans -= c;
}
}
cout << ans;
}
바이오칩
문제 링크: oj.uz인데, 이 문제에 한해 지문이 한글이고 데이터가 더 강하다.
얼마 전에 공부한 트리 DP 최적화 기법을 적용할 수 있길래 기쁜 마음으로 풀었다.
풀이
$\mathrm{dp}(u,x):=T_u$에 대해 조건 하에 $x$개를 뽑았을 때 최댓값.
각 노드 $u$에 대해 다음을 시행하면 된다.
$c\in C_u:$
$\;\;x=\min \{m,|T_u|\}, \cdots, 2,1:$
$\displaystyle \;\;\;\;\mathrm{dp}(u,x)\leftarrow \max \left \{ \mathrm{dp}(u,x), \max_{0\le y\le \min \{x,|T_c|\}} \left \{ \mathrm{dp}(c,y) + \mathrm{dp}(u,x-y) \right \}\right \}$
시간 복잡도 계산이 중요하다.
$O\left (\min \{m,|T_u|\} \times \min \{m,|T_v|\}\right )$ 시간에 두 트리를 합치고 있으므로 문제를 푸는 전체 시간 복잡도는 $O(nm)$이다.
#include <bits/stdc++.h>
using namespace std; using ii = pair<int,int>; using ll = long long;
#define rep(i,a,b) for (auto i = (a); i <= (b); ++i)
#define per(i,a,b) for (auto i = (b); i >= (a); --i)
#define all(x) begin(x), end(x)
#define siz(x) int((x).size())
#define Mup(x,y) x = max(x,y)
#define mup(x,y) x = min(x,y)
#define fi first
#define se second
#define dbg(...) fprintf(stderr,__VA_ARGS__)
const int N = 2e5+3, M = 503;
int n, m, a[N], r, sub[N];
vector<int> child[N];
vector<ll> dp[N];
void pre(int s = r, int e = 0) {
sub[s] = 1;
for (auto u : child[s]) if (u != e) {
pre(u,s), sub[s] += sub[u];
}
}
void solve(int s = r, int e = 0) {
dp[s].resize(min(m,sub[s])+1);
dp[s][0] = 0;
for (auto u : child[s]) if (u != e) {
solve(u,s);
per(x,1,min(m,sub[s])) rep(y,0,min(x,sub[u])) {
Mup(dp[s][x],dp[u][y]+dp[s][x-y]);
}
}
Mup(dp[s][1],ll(a[s]));
}
int main() {
scanf("%d %d", &n, &m);
rep(i,1,n) {
int p; scanf("%d %d", &p, &a[i]);
if (p == 0) r = i;
else child[p].push_back(i);
}
pre(), solve();
printf("%lld", dp[r][m]);
}'PS 기록들' 카테고리의 다른 글
| 2023년 상반기 알고리즘 대회 운영/출제/검수 경험 공유 ★ (2) | 2023.06.27 |
|---|---|
| KOI 2023 고등부 1차 풀이 및 후기 ★ (2) | 2023.05.15 |
| USACO January 2014 Contest (0) | 2023.02.21 |
| JOI 22/23 Finals Online Contest 후기 (0) | 2023.02.15 |
| Codeforces Round #848 (Div. 2) (0) | 2023.02.02 |

